Расчет параметров диэлектрического волновода

Министерство Российской Федерации по Связи и Информатизации

Московский Технический Университет Связи и Информатики

Кафедра технической электродинамики и антенн

Курсовая работа

Расчет параметров диэлектрического волновода

Москва 2000г.

Задание.

Диэлектрический волновод представляет собой плоскую пластину из диэлектрика, помещенную в безграничную диэлектрическую среду с меньшей диэлектрической проницаемостью (ε_r1>ε_r2). Продольное сечение волновода и система координат показана на рис.1.

По волноводу распространяется монохроматическая волна с частотой f.

Продольная составляющая вектора Hm в пластине (в среде 1) равна:

Hm_z1 = Acos(γx) *e^-iβz,  а над пластиной при (x≥h) равна:

                                                                                             Hm_z2 = Be^-αX * e^-ίβz

   Продольные составляющие вектора Em в указанных средах отсутствуют, т.е. Em_z1=Em_z2=0.

В этих выражениях А и В – некоторые постоянные имеющие размерность А/м, а α и γ – поперечные волновые числа в средах 1 и 2.

   В таблице 1 даны значения среднего за период потока энергии через поперечное сечение либо пл. типы Р_ср1, либо над пластиной Р_ср2 (предполагать, что волновод в этом случае имеет единичную длину по оси у).

                                                                                                Таблица 1.

№№ n/n	μz2 = μz1  = 1,                                      σ2 = σ1 = 0
	εr1	εr2	2h, мм	f, ГГц	Рср1, Вт	Рср2, Вт
3	2,56	1,0	30	10	-	3,2

Требуется:

1.  Записать выражения для всех остальных составляющих векторов поля в средах 1 и 2.

2.  Используя граничные условия при x = h, записать соотношения, связывающие между собой величины А, В, α и γ.

3.  Исключив постоянные А и В, получить уравнение, связывающее между собой поперечные волновые числа α и γ.

4.  Решить данные трансцендентные уравнения графическим способом.

5.  Определить типы волн, распространяющиеся по волноводу.

6.  Для основного типа волны определить α, γ  и β.

7.  Определить фазовую скорость основного типа волны.

8.  Определить постоянные А и В, входящие в выражения составляющих поля.

9.  Рассчитать и построить зависимости всех составляющих полей для основного типа волны при изменении координаты Х (в областях 1 и 2).

1.  Запишем выражения для остальных составляющих векторов поля в средах 1 и 2.

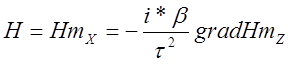    , где  g² для 1-ой среды и  -a² для 2-ой.

   

Из первого уравнения Максвелла следует, что

 

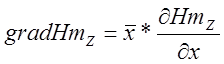
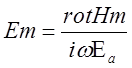
Запишем выражения для остальных составляющих векторов поля в 1-ой среде:

 ;

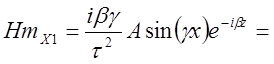
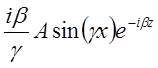
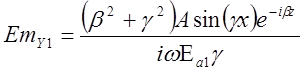
во 2-ой среде:

 ;

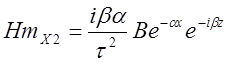
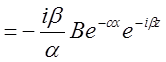
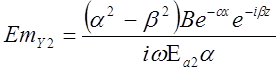
2.  Запишем отношения, связывающие между собой величины А, В, a и g, используя граничные условия при x = h:

 Hm_Z1½_{x = h} = Hm_Z2½_{x = h}

 Em_Y1½_{x = h} = Em_Y2½_{x = h}

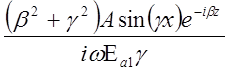
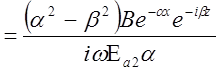                     (система 1.)

3. Проведя сокращение, получим:

Найдем пару для решения системы уравнения, используя уравнение:

 для первой среды

   для второй среды, где к₁ и к₂ – волновые числа.

, где  E_a1=E₀×E_r1=22.656×10^-12 Ф/м

, где  E_a1=E₀×E_r1=8.85×10^-12 Ф/м

m_a1=m_a2=m_r2= 1.256×10^-6 Гн/м, тогда

к₁ = 335.001; к₂ = 209.3756

 

Решаем уравнения:

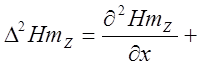
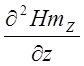
для 1-ой среды:

; ;

;

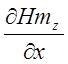
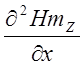
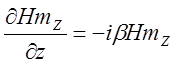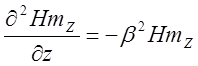
следовательно:

преобразуем это выражение и получим в итоге следующее:

Для второй среды вычисления аналогичны:

=_; 

 

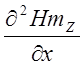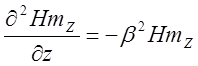
Вычтем из первого второе и домножим на h²

 

h²×½½×h²

h²

В итоге получаем систему уравнений, решение которой будем находить графически:

h²

4. Решим эту  систему.  Введем обозначения:

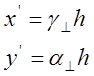;  R= = 3.922651  R² = 15.3879

Построим график:

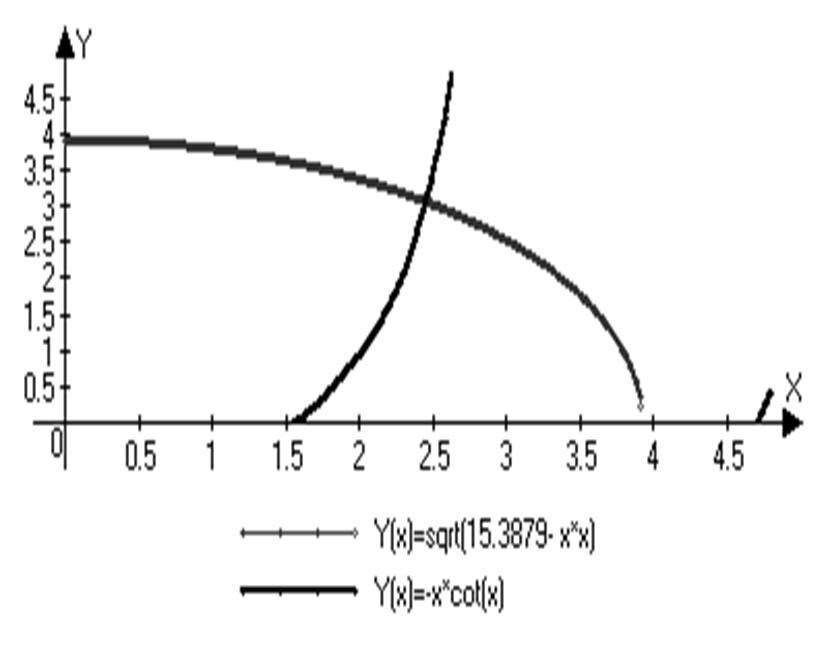5. Соответственно решением данной системы является точка С(2.5; 3). Эта точка пересечения является единственным решением данной системы, поэтому можно сказать, что в волноводе распространяется одна волна H₁ и она нечетная.

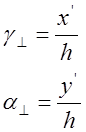
6. Зная значения x’ и y^’, найдем значения g и a:

  a= 203.33; g=164

значение b находим из уравнений:

 

  b @ 292

7. Зная значение b, рассчитаем фазовую скорость: V_ф=w/b=0.125×10⁹ м/с

8. Определим постоянные А и В.

Р₂=2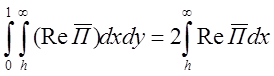, где ReП – действительная часть вектора Пойтинга

Вектор Пойтинга: 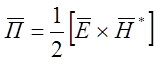, где

;

;

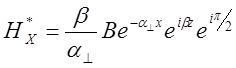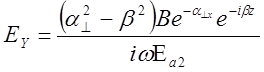
В нашем случае у вектора Н отсутствует y-овая составляющая, а у вектора Е – х-овая и z-овая составляющие, поэтому вектор Пойтинга будет выглядеть следующим образом:

 

 

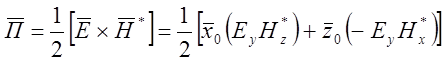
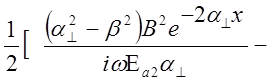
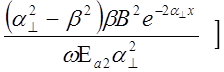
Р₂ = 2 = = = =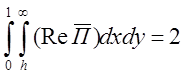

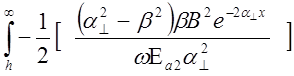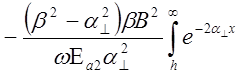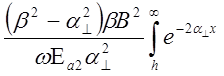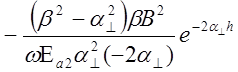
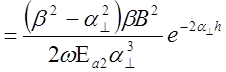
Р₂ = 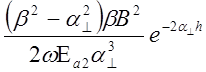  В = 1.527 A/m

Из первого уравнения системы 1 найдем значение постоянной А. Воспользуемся граничными условиями при x = h

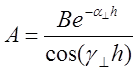   = 0.0724 A/m

А = 0.0724 A/m

В = 1.527 A/m

9.Определив значение постоянных А и В, построим графики зависимости всех составляющих полей для основного типа волны при изменении координаты Х.

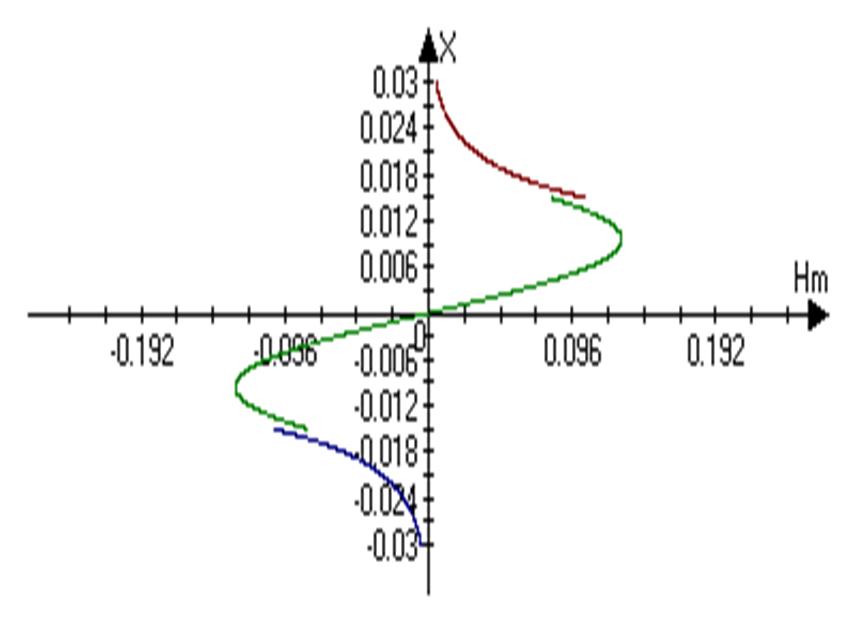
Построим график зависимости составляющей Hm_x

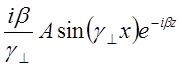=0.1289sin(164x)

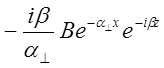= -2.1929exp(-203.33x)

Построим график зависимости составляющей Еm_y

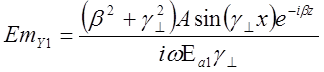=34.7832sin(164x)

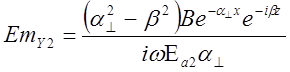=-593.267exp(-203.33)

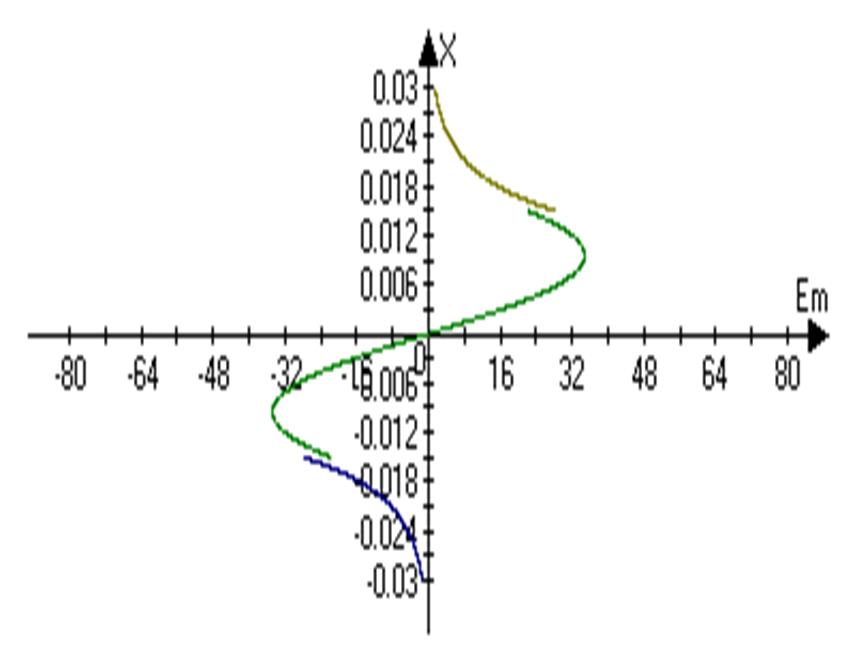
Построим график зависимости составляющей Hm_z

 =0.0724cos(164x)

= 1.527exp(-203.33)

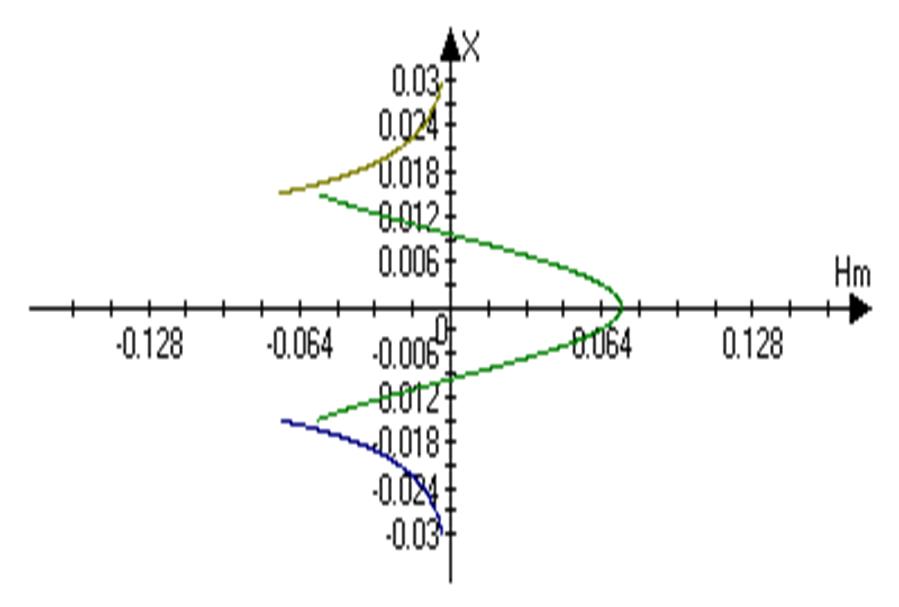
P.S. Графики не совсем верны, т.к. строились не в радианной, а в градусной мере. Лучше всего их строить в ручную, тогда Гайнутдинов(если знаете такого) не придираетсяJ