Резонанс в электрических цепях. Основные сведения. Резонанс в последовательном контуре

3. Лабораторная работа № 3

РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

3.1. Основные сведения

В теории колебаний резонансом называется процесс вынужденных колебаний с такой частотой, при которой интенсивность колебаний при прочих равных условиях максимальна. Характеризовать интенсивность колебательного процесса можно по разным проявлениям, которые могут достигать максимума при различных частотах. Поэтому для каждой колебательной системы необходимо условиться о критерии резонанса. 

В линейных ЭЦ с двумя дуальными реактивными элементами       (L и C) на определенной частоте гармонического воздействия возникают резонансные явления, проявлением которых являются максимальные амплитуды токов или напряжений на элементах цепи.

3.1.1. Резонанс в последовательном контуре

Электрическую цепь, содержащую последовательно соединенные резистивный, индуктивный и емкостной элементы называют последовательным контуром или RLC-цепью (рис. 4.1). Комплексное сопротивление последовательного контура равно

,                               (3.1)

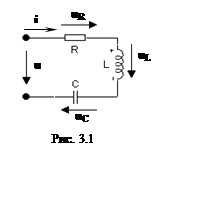где r = R + R_L + R_C – активное сопротивление цепи, обусловленное резистивным элементом, а также потерями в катушке индуктивности (R_L) и конденсаторе (R_C), x = (x_L – x_C) = (ωL – 1/ωC) – реактивное сопротивление цепи, - модуль, а φ = arctg(x/r) – аргумент комплексного сопротивления.

Если на некоторой частоте  гармонического воздействияω₀ реактивная составляющая сопротивления цепи равна нулю (x = 0), то в последовательном контуре наступает резонанс. Поскольку при x = 0 имеем ω₀L = 1/ω₀C, то резонансная угловая частота ω₀ определяется по формуле

.                                                                                      (3.2)

Поскольку при резонансе x_L = x_C и комплексные сопротивления  и отличаются только фазой, то комплексные напряжения на индуктивности и емкости равны по модулю и противоположны по фазе:

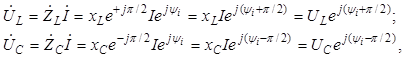         (3.3)

где - комплексный ток, протекающий в цепи.

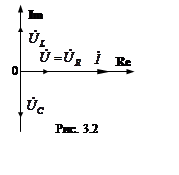Векторная диаграмма последовательного контура в режиме резонанса приведена на рис. 3.2, а резонанс в рассматриваемой цепи называется резонансом напряжений. Из (3.1) следует, что при ω = ω₀  входное сопротивление цепи . Поэтому напряжение на входных выводах цепи равно напряжению на активном сопротивлении R и совпадает  по фазе с входным током (рис. 3.2):

.               (3.4)

Кроме того, полное сопротивление цепи z при x = 0 минимально:, а ток I при заданном напряжении U достигает наибольшего значения I = U/R. Напряжения на индуктивности и емкости при резонансе могут значительно превышать входное напряжение:

.                                (3.5)

Учитывая выражение (3.2) можно записать

.                                                                (3.6)

Величина ρ называется характеристическим сопротивлением RLC-цепи. Подставив в выражения (3.5) значение  ρ (3.6) получим:

.                                                               (3.7)

Отношение напряжения на индуктивности или емкости последовательного контура к напряжению входного воздействия называется добротностью контура (Q) или коэффициентом резонанса.

Обычно Q >> 1, поэтому  добротность  контура  указывает,  во сколько раз напряжение на индуктивном или емкостном элементе при резонансе больше, чем напряжение на входных выводах. Из (3.5) так же следует: Q = ω₀L/R = 1/(ω₀CR).

Пусть к колебательному контуру приложено синусоидальное напряжение u = U_msinωt, амплитуда которого U_m неизменна, а частота ω меняется в пределах от 0 до ∞. Изменение частоты приводит к изменению параметров контура: изменяются реактивные составляющие сопротивлений, а следовательно, модуль и фаза комплексного сопротивления цепи. Зависимости параметров ЭЦ от частоты называются частотными характеристиками цепи. Частотные характеристики последовательного контура (рис.3.1) x_L(ω), -x_C(ω) и   x(ω) = x_L(ω) - x_C(ω), показаны на рис. 3.3. Изменение реактивного сопротивления приводит к изменению тока и напряжений на элементах ЭЦ, т.е. к изменению режима цепи. 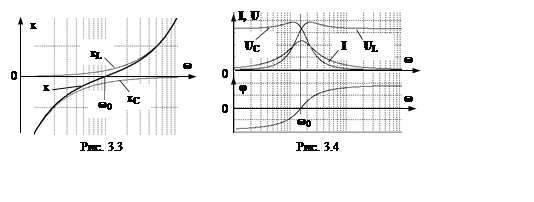Зависимости амплитудных или действующих значений тока и напряжения от частоты называются резонансными кривыми. На рис. 3.4 представлены резонансные кривые последовательного контура (Q = 1): I(ω), U_L(ω) и U_C(ω), а также фазовый сдвиг между входным напряжением и током - кривая  φ(ω). Из приведенных выше графиков видим, что при ω < ω₀ реактивное сопротивление контура x = x_L – x_C носит емкостной характер, фазовый сдвиг –π/2 <φ <0, а U_C > U_L. При ω > ω₀ результирующее реактивное сопротивление контура x > 0 и носит индуктивный характер, фазовый сдвиг 0 < φ < π/2, а U_C < U_L. При резонансе (ω = ω₀) действующие значения напряжений U_C и U_L равны между собой, фазовый сдвиг φ = 0, а входной ток I достигает максимума.