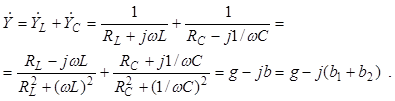 (3.15)
(3.15)
Резонанс в параллельном контуре наступает, если у входной проводимости реактивная составляющая равна нулю:
![]()
![]() или
или
![]() , (3.16)
, (3.16)
где 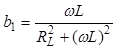 и
и 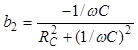 -
реактивные проводимости ветвей. Подставив в соотношение (3.16) значения b1 и b2 ,
выраженные через параметры цепи, и решив полученное уравнение относительно ω,
найдем значение для резонансной частоты:
-
реактивные проводимости ветвей. Подставив в соотношение (3.16) значения b1 и b2 ,
выраженные через параметры цепи, и решив полученное уравнение относительно ω,
найдем значение для резонансной частоты:
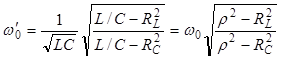 , (3.17)
, (3.17)
Из
(3.17) следует, что не при всех параметрах параллельного контура может быть
достигнут резонанс. Резонанс возможен, если сопротивления RL
и RC оба больше или оба меньше
характеристического сопротивления параллельного контура ![]() .
В противном случае получается мнимая частота ω’0, т.е. не существует
такой частоты, при которой имел бы место резонанс. При RL
= RC ≠ ρ резонансная
частота ω’0= ω0, т.е. такая же, как и при резонансе в
последовательном контуре.
.
В противном случае получается мнимая частота ω’0, т.е. не существует
такой частоты, при которой имел бы место резонанс. При RL
= RC ≠ ρ резонансная
частота ω’0= ω0, т.е. такая же, как и при резонансе в
последовательном контуре.
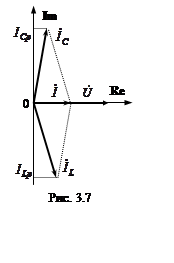 В радиотехнике и
электросвязи применяются контуры с малыми потерями, т.е. RL
(RC) << ρ.
В этом случае величинами сопротивлений RL и
RC в (3.17) можно пренебречь и резонансную
частоту вычислить по формуле
В радиотехнике и
электросвязи применяются контуры с малыми потерями, т.е. RL
(RC) << ρ.
В этом случае величинами сопротивлений RL и
RC в (3.17) можно пренебречь и резонансную
частоту вычислить по формуле ![]() .
.
Из векторной диаграммы (рис. 3.7) видно, что при резонансе (b2 = -b1) противоположные по фазе реактивные составляющие токов в ветвях равны. Поэтому резонанс в рассматриваемой цепи получил название резонанса токов. Входной ток при этом может быть значительно меньше токов в ветвях и совпадает по фазе с напряжением на входе контура.
Таким образом, и в параллельном, и в последовательном контурах при резонансе наблюдается совпадение по фазе тока и напряжения на входных зажимах двухполюсника, что может быть принято в качестве критерия режима «резонанс» в пассивных двухполюсниках, содержащих катушки индуктивности и конденсаторы. В литературе данный критерий резонанса получил название «фазовый резонанс» [1].
Сопротивления потерь RL и RC (рис. 3.6) можно заменить параллельно подключенными к индуктивности и емкости эквивалентными сопротивлениями RэкL и RэкС, вычисленными вблизи резонанса по формулам [2]:
![]() ;
; ![]() . (3.18)
. (3.18)
Тогда проводимость G потерь контура (при ω ≈ ω0) равна
![]() . (3.19)
. (3.19)
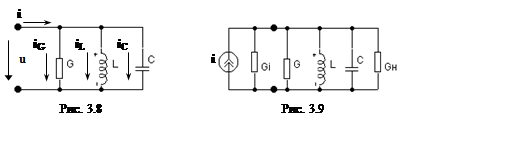
Схема замещения параллельного контура при использовании параллельных схем замещения катушки индуктивности и конденсатора приведена на рис. 3.8. На резонансной частоте с учетом формулы (3.2) полные проводимости индуктивности и емкости равны:
![]() ;
; ![]() , где σ = 1/ρ
– характеристическая проводимость параллельного колебательного контура
(величина, обратная характеристическому сопротивлению контура).
, где σ = 1/ρ
– характеристическая проводимость параллельного колебательного контура
(величина, обратная характеристическому сопротивлению контура).
 |
![]() . (3.20)
. (3.20)
Из
выражения (3.20) следует, что с увеличением проводимости G
потерь добротность параллельного колебательного контура падает. Схема замещения
параллельного контура, приведенная на рис. 3.8, существенно упрощает процесс
анализа его свойств. В этом случае можно использовать все выражения, полученные
для последовательного колебательного контура, производя в них взаимные замены
токов и напряжений, сопротивлений и проводимостей элементов схемы. В частности,
выражение входной проводимости параллельного контура ![]() и
выражение (3.1), определяющее входное сопротивление последовательного контура,
имеют одинаковую структуру и могут быть получены одно из другого путем
упомянутых замен.
и
выражение (3.1), определяющее входное сопротивление последовательного контура,
имеют одинаковую структуру и могут быть получены одно из другого путем
упомянутых замен.
Эквивалентная добротность контура (рис. 3.9) при подключении к нему источника энергии (с внутренней проводимости Gi) и нагрузки (с проводимостью GН) определяется выражением (3.20) при замене G на Gэк = G + Gi + GH:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.