Резонанс в электрических цепях. Основные сведения. Резонанс в последовательном контуре, страница 2

График зависимости тока I от частоты (рис. 3.4) показывает, что рассматриваемая цепь обладает «избирательными свойствами». Если на вход такого контура подать сумму гармонических колебаний различных частот, но с одинаковыми амплитудами, то на выходе обнаружим, что амплитуда колебаний с частотой, близкой к резонансной, значительно превышает амплитуду колебаний, частота которых существенно отличается от резонансной. В электросвязи и радиотехнике широко используются избирательные свойства таких цепей, а режим резонанса является нормальным режимом работы.

Избирательная цепь характеризуется полосой пропускания  (шириной полосы пропускания), которая определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает больше, чем в α раз, относительно своего максимального значения:

   ,                                                     (3.8)

где ω_В = 2πf_В и ω_Н = 2πf_Н – верхняя и нижняя граничные частоты.

Обычно полосу пропускания находят на уровне, когда амплитуда отклика составляет  от максимального значения (α = 1,4). Можно показать [2], что полоса пропускания контура на уровне 0,707 равна

  ,                                                               (3.9)

т.е. полоса пропускания контура определяется его добротностью.

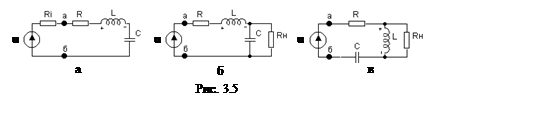
Рассмотрим влияние внутреннего сопротивления R_i источника гармонического воздействия и нагрузки R_н на избирательные свойства последовательного колебательного контура (рис. 3.5). Схему с реальным источником напряжения (рис. 3.5, а) можно привести к виду (рис. 3.1), если заменить последовательно соединенные сопротивления R_i и R эквивалентным сопротивлением R_эк1 = R_i.+ R. Тогда эквивалентная добротность последовательного контура определится выражением

,                                      (3.10)

где Q = ρ/R – добротность контура без учета сопротивления источника, а ширина полосы пропускания увеличивается до значения:

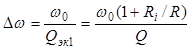.                                                            (3.11)

Сопротивления нагрузки R_Н, подключенные параллельно емкости или индуктивности (рис. 3.5, б, в), могут быть заменены последовательно включенными с емкостью или индуктивностью сопротивлениями (R_НС и R_НL), вычисленными по формулам [2]:

   .                                      (3.12)

Сопротивления R_НС и R_НL, учитывающие влияние нагрузки на работу контура, называются внесенными в контур сопротивлениями нагрузки. На частотах, близких к резонансной (ω ≈ ω₀), выражения (3.12) с учетом (3.6) можно преобразовать к виду:

.                                                            (3.13)

Влияние сопротивления R’_H на параметры контура аналогично влиянию внутреннего сопротивления источника R_i, т.е. R_эк2 = R’_H + R. Далее можно воспользоваться формулами (3.10) и (3.11) или используя соотношение (3.13) преобразовать их к виду

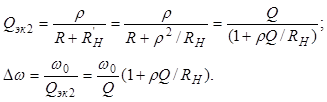                            (3.14)

Выражения (3.14) позволяют определить  параметры (добротность и полосу пропускания) последовательного контура с учетом сопротивления подключенной к контуру нагрузки (R_Н).

Проведенный анализ показывает, что для повышения эквивалентной добротности контура (уменьшения полосы пропускания) необходимо использовать источник энергии с минимальным внутренним сопротивлением R_i, а сопротивление нагрузки R_Н должно быть как можно большим.

4.1.2. Резонанс в параллельном контуре

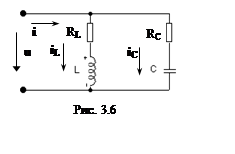Параллельным контуром называется электрическая цепь, состоящая из параллельно соединенных катушки индуктивности и конденсатора. Поскольку в реальных конденсаторах и катушках индуктивности имеет место потеря энергии, преобразуемой в тепло, то эквивалентная электрическая схема рассматриваемого контура представляет собой электрическую цепь (рис. 3.6), содержащую две параллельные ветви с комплексными проводимостями  и . Сопротивления R_L и R_C определяют тепловые потери в ветвях контура.

Входная проводимость параллельного контура равна: