Граничные условия на поверхности раздела сред

 

                                    2.1.                                    Граничные условия для нормальных составляющих векторов электромагнитного поля.

                                               

2.2.

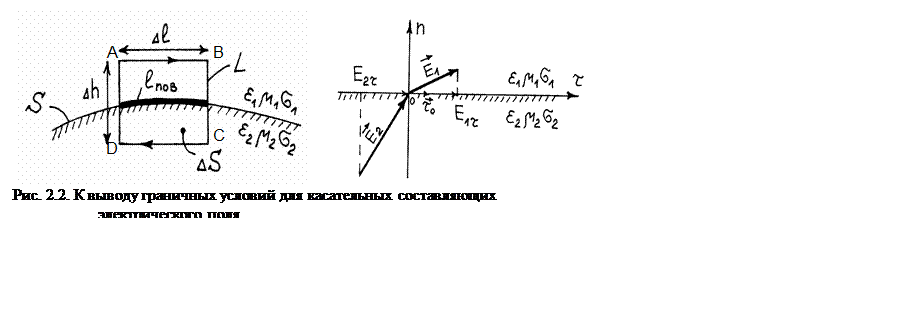
Граничные условия для касательных  составляющих векторов электромагнитного поля.

 

2.3.

Граничные условия на поверхности идеального диэлектрика и идеального проводника.

 

2. Граничные условия на

поверхности раздела сред

При решении практических задач электродинамики помимо уравнений Максвелла необходимо также знать граничные условия, т.е. знать соотношения между векторами поля в двух очень близких точках, находящихся по обе стороны границы раздела сред. Если на границе между различными материальными средами параметры среды e, m, s скачкообразно изменяются, то, очевидно, векторные функции , ,  и  будут иметь разрывы. Определить характер этих разрывов и означает задать граничные условия на поверхности раздела сред. Поскольку разрывные функции нельзя дифференцировать, то для нахождения соотношений поля на границе раздела, необходимо использовать интегральные уравнения Максвелла и предельные переходы.

 

2.1. Граничные условия для нормальных

 составляющих векторов электромагнитного поля

Формулируется закон поведения нормальных составляющих векторов поля на границе раздела двух сред.

 

Рассмотрим плоскую границу раздела двух сред с параметрами e_a1, m_a1, s₁  и  e_a2,  m_a2,  s_2. На поверхности раздела сред выделим достаточно малый элемент  DS , в пределах которого в обеих средах нормальные составляющие вектора  равномерно распределены. На основании DS построим цилиндр с высотой  h  так, чтобы его основания находились  в разных средах, как показано на рис.2.1.

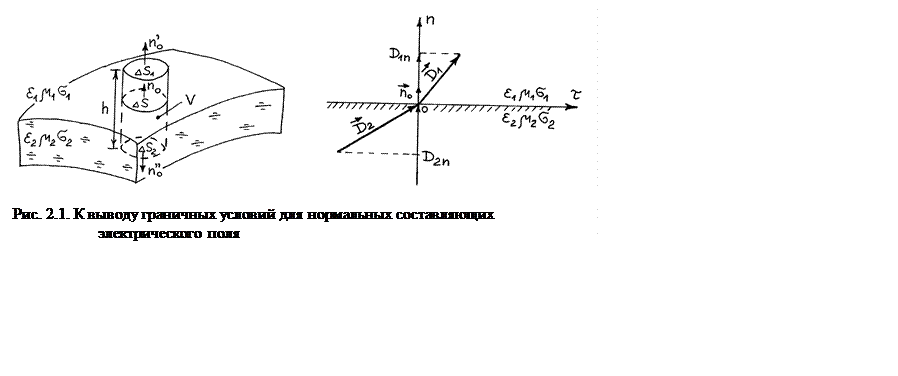Используем третье уравнение Максвелла в интегральной форме:

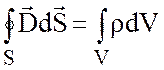, где: – единичный вектор, нормальный к ; – нормаль к .

Разобьем интеграл по замкнутой поверхности S, ограничивающей объем V, на три интеграла:

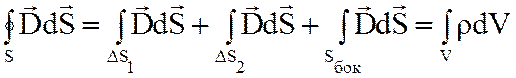.                          (2.1)                                                                                                                                                                                                      

Устремим высоту цилиндра h к нулю, тогда:

 ;                        ;

 ;                            .

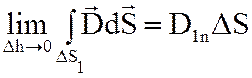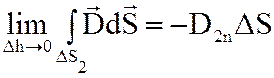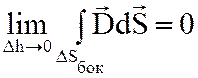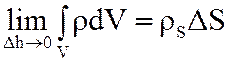Отсюда

 ,                                               (2.2)

где  - плотность поверхностного заряда. Эта величина вводится чисто формально. Реально

.                                                    (2.3)

Нормальная составляющая вектора электрической индукции на границе раздела непрерывна .

Поскольку из материальных уравнений , то граничные условия для нормальной составляющей вектора напряженности электрического поля будут иметь вид:

e_а1Е_1n - e_а2Е_2n = 0                                               (2.4)

или

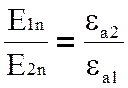.                                                       (2.5)

Из (2.5) следует:

 Нормальная составляющая вектора   на границе раздела двух сред  

 терпит скачок, равный отношению диэлектрических проницаемо-

 стей  сред.

Рассмотрим теперь граничные условия для нормальных составляющих магнитного поля. Для этого по аналогии охватим обе среды цилиндром с объемом V и используем четвертое уравнение Максвелла в интегральной форме:

.

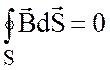Разобьём замкнутый интеграл по поверхности на три интеграла:

.

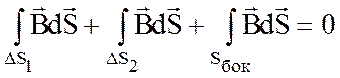Устремим h к нулю, тогда:

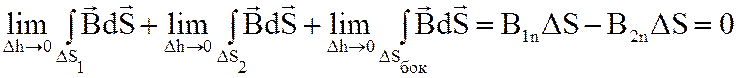
или

.                                                      (2.6)

Таким образом:

Нормальная составляющая вектора магнитной индукции при переходе через границу раздела двух сред остается непрерывной.

Поскольку из материальных уравнений , то граничные условия для нормальных составляющих вектора напряженности магнитного поля имеют вид:

m_а1Н_1n = m_а2Н_2n                                                              (2.7)        

или

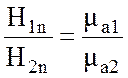.                                                      (2.8)

Из (2.7) следует, что   

Нормальная составляющая вектора  на границе сред терпит разрыв, величина которого равна отношению абсолютных магнитных проницаемостей сред.

 

2.2. Граничные условия для касательных

 составляющих векторов электромагнитного поля

Формулируется закон поведения касательных составляющих векторов поля на границе раздела двух сред.

Рассмотрим плоскую границу раздела двух сред с параметрами e_а1, m_а1, s₁  и  e_а2, m_а2, s₂. Охватим обе среды контуром , плоскость которого перпендикулярна поверхности раздела двух сред (см. рис.2.2.), причем .

        Используем второе уравнение Максвелла в интегральной форме:

.

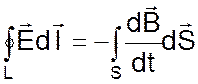Разобьем контур  на четыре участка, тогда:

.

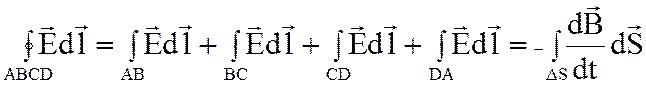(2.9)

З десь  - площадь, ограниченная контуром ABCD. Устремим высоту контура Δh к нулю, тогда в пределе стороны АВ и CD совпадут с . Используя условие малости , получим:

,        ,        .

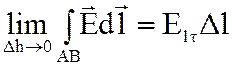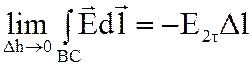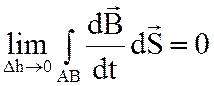Окончательно:    ,   или

Е_1t = Е_{2t .}                                                    (2.10)

Касательная составляющая вектора напряженности электрического поля непрерывна на границе раздела сред.

Используя материальное уравнение , получим:

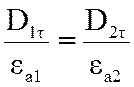                                                 (2.11)

или                                             .                                          

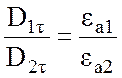Касательная составляющая вектора  терпит разрыв, величина которого определяется соотношением диэлектрических проницаемостей обеих сред.

Рассмотрим граничные условия для касательных составляющих вектора напряженности магнитного поля . По аналогии с предыдущим случаем, охватим границу раздела сред контуром ABCD и используем первое уравнение Максвелла:

.

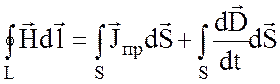Разбиваем интеграл по замкнутому контуру L на четыре интеграла: