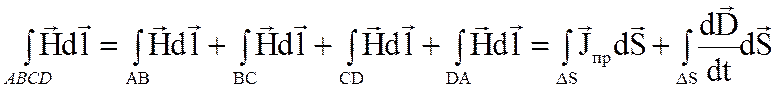 .
.
(2.12)
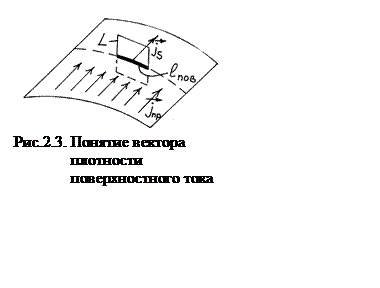 По аналогии с (2.2) получим:
По аналогии с (2.2) получим:
![]() , где
, где
![]() - плотность поверхностного тока. Эта
величина как
- плотность поверхностного тока. Эта
величина как ![]() в случае электрического поля, имеет чисто
формальный смысл. Поэтому реально:
в случае электрического поля, имеет чисто
формальный смысл. Поэтому реально:
![]() . (2.13)
. (2.13)
![]() Касательная
составляющая вектора напряженности магнитного поля на границе раздела сред
претерпевает скачок, численно равный поверхностной плотности тока проводимости,
протекающего по границе раздела сред.
Касательная
составляющая вектора напряженности магнитного поля на границе раздела сред
претерпевает скачок, численно равный поверхностной плотности тока проводимости,
протекающего по границе раздела сред.
Используя материальное уравнение ![]() , определим
граничные условия для касательных составляющих вектора магнитной индукции:
, определим
граничные условия для касательных составляющих вектора магнитной индукции:
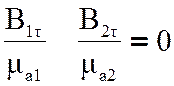 , (2.14)
, (2.14)
откуда
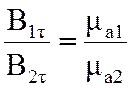 .
.
![]() Касательная составляющая вектора магнитной
индукции на границе
Касательная составляющая вектора магнитной
индукции на границе
раздела двух сред терпит скачок, равный отношению магнитных про-
ницаемостей сред.
2.3. Граничные условия на поверхности идеального
диэлектрика и идеального проводника
Рассматриваются частные случаи применения граничных условий часто используемые для решения практических задач.
Выпишем полученные в разделах 2.1 и 2.2 граничные условия для нормальных и касательных составляющих электромагнитного поля.
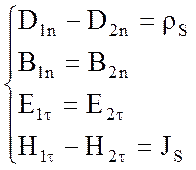 . (2.15)
. (2.15)
Данные уравнения составляют полную систему граничных условий, которые справедливы для любых электромагнитных процессов, рассматриваемых в классической (макроскопической) электродинамике.
При изучении переменных электромагнитных полей вблизи некоторых диэлектрических и металлических тел часто предполагают, что рассматриваемые тела являются идеальным диэлектриком или идеальным проводником. В этом случае граничные условия (2.9) упрощаются.
Рассмотрим граничные условия на поверхности идеального
диэлектрика. Поскольку для идеального диэлектрика удельная проводимость s = 0, то плотность тока проводимости ![]() и, следовательно, поверхностный ток отсутствует,
и, следовательно, поверхностный ток отсутствует, ![]() . Поэтому
для данного частного случая получаем:
. Поэтому
для данного частного случая получаем:
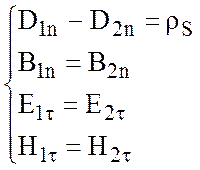 .
(2.16)
.
(2.16)
Рассмотрим теперь граничные условия на поверхности
идеального проводника. Для идеального проводника s = ¥, следовательно, и вектор плотности тока проводимости ![]() тоже
стремится к бесконечности при некотором конечном
тоже
стремится к бесконечности при некотором конечном ![]() . Это
означает, что появление такого большого тока должно быть связано с бесконечно
большой энергией поля, чего при источниках, имеющих конечную мощность, быть не
может. Поэтому, исходя из закона сохранения энергии, следует предположить, что внутри
идеального проводника переменное электрическое поле существовать не может,
т.е.
. Это
означает, что появление такого большого тока должно быть связано с бесконечно
большой энергией поля, чего при источниках, имеющих конечную мощность, быть не
может. Поэтому, исходя из закона сохранения энергии, следует предположить, что внутри
идеального проводника переменное электрическое поле существовать не может,
т.е. ![]() . Исходя из
первого уравнения Максвелла при
. Исходя из
первого уравнения Максвелла при ![]() получаем, что и вектор
получаем, что и вектор ![]() тоже равен нулю, а из материальных уравнений находим,
что
тоже равен нулю, а из материальных уравнений находим,
что ![]() .
.
Следовательно, внутри идеального проводника переменное электромагнитное поле отсутствует (более подробно это явление мы рассмотрим позднее в разделе 6.)
Таким образом, граничные условия на поверхности идеального проводника имеют вид:
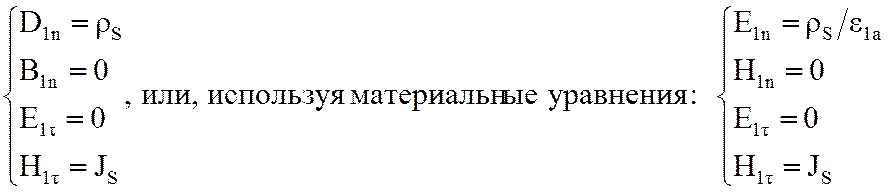 .
.
(2.17)
Поскольку в дальнейших разделах мы часто будем обращаться к этим граничным условиям, остановимся на уравнениях (2.11) более подробно. Непосредственно из этих уравнений вытекает:
1.
Вектор напряженности
электрического поля вблизи поверхности проводника направлен перпендикулярно к
поверхности и равен ![]() (см. рис.2.4.).
(см. рис.2.4.).
2. Вектор напряженности магнитного поля вблизи поверхности проводника направлен по касательной к поверхности проводника и равен jS (см. рис.2.4.).
3. Равенство нулю касательной составляющей электрического поля является следствием отсутствия поля внутри проводника.
 Последнее требует пояснения. Отсутствие поля внутри
проводника означает отсутствие внутри проводника объемных зарядов. Это в свою
очередь означает, что заряд проводника концентрируется на его поверхности в
слое атомарной толщины. Конечно, внутри проводника имеются как положительные,
так и отрицательные заряды, но они взаимно компенсируются и в целом внутренние
области проводника нейтральны. Установ-ление этой нейтральности происходит
чрез-вычайно быстро. Рассмотрим в этой связи некоторый объем проводника
(например, медного) и предположим, что в момент времени t = 0
плотность свободных зарядов в нем отлично от нуля. Используем закон сохранения
заряда (см. подробнее раздел 1.7.):
Последнее требует пояснения. Отсутствие поля внутри
проводника означает отсутствие внутри проводника объемных зарядов. Это в свою
очередь означает, что заряд проводника концентрируется на его поверхности в
слое атомарной толщины. Конечно, внутри проводника имеются как положительные,
так и отрицательные заряды, но они взаимно компенсируются и в целом внутренние
области проводника нейтральны. Установ-ление этой нейтральности происходит
чрез-вычайно быстро. Рассмотрим в этой связи некоторый объем проводника
(например, медного) и предположим, что в момент времени t = 0
плотность свободных зарядов в нем отлично от нуля. Используем закон сохранения
заряда (см. подробнее раздел 1.7.):
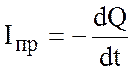 , или
, или 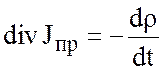 . (2.18)
. (2.18)
Так
как ![]() , то
, то ![]() или,
используя материальное уравнение,
или,
используя материальное уравнение, ![]() , а
, а ![]() . Подставляя в (2.12) получим:
. Подставляя в (2.12) получим:
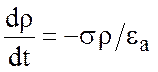 , где:
eа = eо×e - абсолютная диэлектрическая проницаемость среды.
, где:
eа = eо×e - абсолютная диэлектрическая проницаемость среды.
Решение данного дифференциального уравнения первого порядка имеет вид:
![]() , то
есть объемная плотность заряда уменьшается экспоненциально. Можно считать, что
образовавшийся объемный заряд "рассасывается" в течение промежутка
времени
, то
есть объемная плотность заряда уменьшается экспоненциально. Можно считать, что
образовавшийся объемный заряд "рассасывается" в течение промежутка
времени ![]() ,
называемого временем релаксации. Для нашего примера, учитывая, что у
меди (см. табл.1.1.) s = 5,65×107 См/м,
получим t » 10-19 с. Такой
промежуток времени чрезвычайно мал даже в масштабах внутриатомных процессов. Поэтому
с большой точностью можно считать, что в проводнике свободные заряды
распределены по поверхности, а объемные заряды отсутствуют.
,
называемого временем релаксации. Для нашего примера, учитывая, что у
меди (см. табл.1.1.) s = 5,65×107 См/м,
получим t » 10-19 с. Такой
промежуток времени чрезвычайно мал даже в масштабах внутриатомных процессов. Поэтому
с большой точностью можно считать, что в проводнике свободные заряды
распределены по поверхности, а объемные заряды отсутствуют.
Пример 2.1. Угол ![]() между вектором
между вектором ![]() и нормалью составляет 300,
и нормалью составляет 300, ![]() ,
, ![]() .
Определить угол
.
Определить угол ![]() между вектором
между вектором ![]() и нормалью.
и нормалью.
Из рисунка 2.2.:
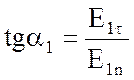 ,
, 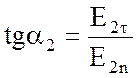 .
.
Так
как, согласно (2.10) ![]() , то
, то ![]() . При
. При ![]() = 0 получаем:
= 0 получаем:
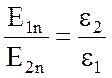 , откуда
, откуда 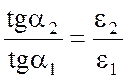 .
.
Тогда
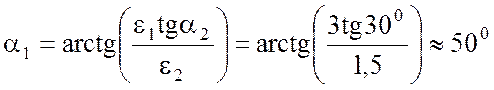 .
.
Вопросы для самопроверки
1. Объяснить механизм образования скачка нормальной составляющей вектора напряженности электрического поля на границе двух сред.
2. Почему в проводниках электромагнитное поле практически отсутствует?
3. Почему линии напряженности электрического поля направлены нормально к границе раздела диэлектрик – проводник?

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.