Вейвлетные пакеты. Волновые пакеты. Основные параметры - частота, масштаб и положение, страница 4

Если библиотека базисов является двоичным деревом, тогда можно найти наилучший базис относительно заданной функции стоимости информации, используя следующий алгоритм. Обозначим   - базисы соответствующие подинтервалу  ,  - наилучший базис для , ограниченный  . Для  существует единственный базис, соответствующий , который, следовательно, является наилучшим: , для всех . Построим  , при  следующим образом

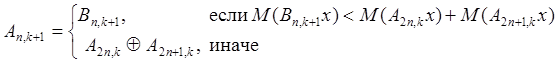 .    (18)

Для иллюстрации алгоритма, рассмотрим пример нахождения наилучшего базиса для 3-х уровневого  дерева вейвлетных пакетов (рис. 5). В прямоугольниках находятся числа, показывающие информационную стоимость этого узла (соответствующего ему набора коэффициентов).

Сначала отметим звездочками нижние ветви дерева (рис. 6).

          Построение дерева начинается с самых нижних узлов. Когда родительский узел имеет более низкую информационную стоимость, чем суммарная информационная стоимость потомков, отмечается родитель. Если наоборот, родитель имеет более высокую информационную стоимость, он отмечается, но ему присваивается более низкая суммарная информационная стоимость потомков. При этом каждый узел рассматривается не более чем два раза – один раз как предок и один раз как потомок.

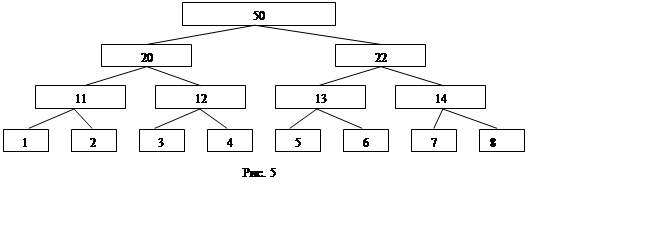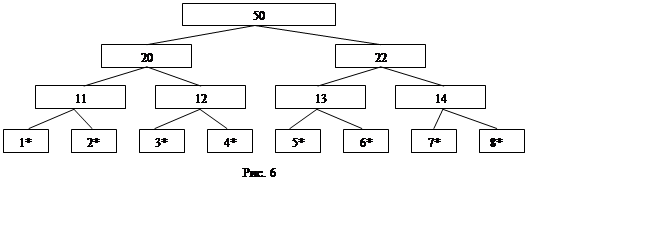Так как анализ дерева начинается с самых нижних узлов,  то информационная стоимость наилучшего базиса ниже любого узла известно до того, как алгоритм поднимется в этот узел. С самым верхним узлом (корнем) будет  связан минимум информационной стоимости среди всех базисов ниже этого узла, то есть наилучшего базиса. Результат проведения этой операции показан на рис. 7. Прежняя информационная стоимость узлов приведена в скобках.

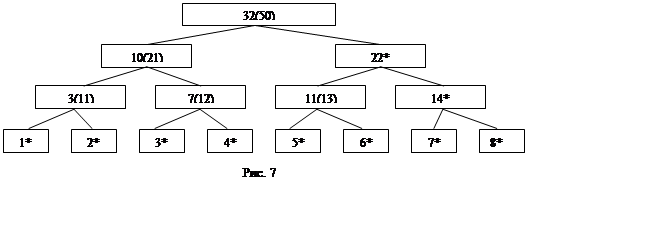После того как все вершины исследованы, необходимо найти те, которые входят в состав наилучшего базиса. Для этого выбирается самый верхний отмеченный узел - он будет входить в состав искомого базис. Часть дерева, исходящая  из этого узла, убирается из дальнейшего рассмотрения. После этого выбирается самый верхний отмеченный узел из оставшихся и т. д. вплоть до самых нижних узлов. На рис. 8  узлы, входящие в наилучший базис, выделены.

Коэффициенты, входящие в наилучший базис, извлекаются из полученных узлов и идентифицируются положением этих узлов в дереве.

Локальные тригонометрические базисы

Рассмотрим построение локальных тригонометрических базисов. Эти базисы представляют собой синусоиды и косинусоиды, промодулированные по амплитуде гладкими кусочными функциями. Полученные библиотеки локальных тригонометрических функций могут быть скомбинированы в древовидную структуру, очень похожую на древовидную структуру вейвлетных пакетов. Аналогично, для этих базисов можно будет найти наилучший базис.

Непрерывные локальные тригонометрические функции

Пусть  - набор непересекающихся интервалов , пронумерованных целым . Построим ортогональный базис, соответствующий разбиению , в котором элементы базиса – косинусоиды, умноженные на гладкие кусочные функции. Интервалы  такие, что их длина не меньше фиксированного положительного числа : . Опишем кусочную функцию, соответствующую этому интервалу, следующим образом

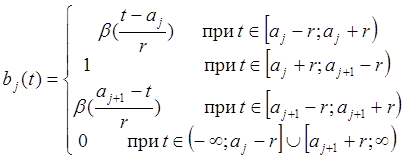,                       (19)

где ; функция  - непрерывная вещественная на , обладающая следующими свойствами:

 при ,

 при ,

  для любых .

В качестве  можно использовать, например, такую функцию .

Набор функций

, где  и , является ортонормированным базисом для . Следовательно, каждый сигнал   может быть представлен в следующем виде

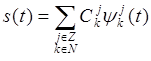,                                                                                  (20)

где

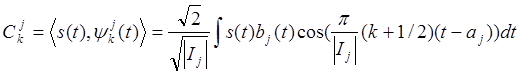.  (21)

График одной из базисных функций для интервала  изображен на рис. 9.