Вейвлетные пакеты. Волновые пакеты. Основные параметры - частота, масштаб и положение, страница 3

При выборе другого подмножества можно получить другой базис. Выбор в качестве базиса какой-нибудь строки полностью, например, (рис 4) , соответствует, грубо говоря, оконному преобразованию Фурье, с шириной окна, зависящей от номера строки. При использовании фильтров Хаара, нижняя строка соответствует базису функций Уолша.

Общее число различных ортогональных базисов, получаемых таким способом, велико, более чем  базисов для .

Метод  «наилучшего базиса»

Определим функцию стоимости информации и найдем из всех базисов в библиотеке тот, который обеспечивает минимум этой функции. Под функцией стоимости информации понимается функция, измеряющая  количество данных, необходимых для описания последовательности. Для заданного сигнала её минимум соответствует тому базису, в котором получается самое эффективное представление, «наилучший» базис.

Можно ввести в качестве функции стоимости различные функционалы для последовательности, но более полезны те, которые измеряют степень концентрации. Под этим подразумевается, что функционал  должен иметь большее значение, когда все элементы последовательности приблизительно одной величины, и меньшее значение, когда часть элементов близка к нулю. Минимизация этого функционала будет соответствовать описанию вектора наиболее экономичным набором коэффициентов.

Этот функционал должен быть определен на единичной сфере, так как будут исследоваться коэффициенты разложения сигнала в различных ортогональных базисах (сумма квадратов этих коэффициентов в различных базисах постоянна и равна энергии сигнала).

          Назовем функционал   для последовательности  аддитивной функцией стоимости, если выполняются условия

 и .

Приведем примеры функционалов, которые могут быть использованы в качестве функции стоимости информации:

1)  Количество элементов, превышающих порог. Установим произвольный порог  и подсчитаем число элементов в последовательности , которые превышают этот порог. Эта величина  дает число коэффициентов, необходимых для передачи сигнала с погрешностью .

2)  Концентрация в   норме, . Выберем произвольный  и примем . В этом случае, чем  меньше величина нормы вектора  с единичной  энергией в , тем больше концентрация энергии вектора в нескольких коэффициентах.

3)  Энтропия. Определим энтропию для последовательности

,                                                    (17.1)

где ;  при .

Это выражение не является аддитивной функцией стоимости, но функция 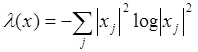 - является. Из соотношения  видно, что минимизация приведет к минимуму . Один из классических вариантов трактовки энтропии: величина  - пропорциональна числу коэффициентов, необходимых для передачи сигнала с фиксированной среднеквадратической ошибкой.         

4)  Логарифм энерги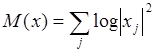и, , при  . Минимизируя этот функционала, можно найти базис Карунена-Лоэва для данного сигнала.

Введем следующее определение:

Библиотека ортонормированных  базисов является бинарным деревом, если она удовлетворяет следующим условиям:

-подмножество элементов базиса может быть отождествлено с интервалом в форме , для ;

-каждый базис в библиотеке соответствует непересекающемуся покрытию интервалами ;

-если  - подпространство базисов, отождествляемое  с интервалом  , то .

Рассмотренное ранее дерево вейвлетных пакетов удовлетворяет этим условиям.

Пусть функционал  задан,  - исходный вектор,  - ортонормальный базис из библиотеки,  - последовательность коэффициентов для вектора  в базисе . Тогда наилучшим базисом для  относительно , есть тот базис , для которого значение  - минимальное.