Вейвлетные пакеты. Волновые пакеты. Основные параметры - частота, масштаб и положение

Вейвлетные пакеты

Волновые пакеты.

 Волновой пакет - это интегрируемое с квадратом модулированное колебание, хорошо локализованное и по частоте и по временному положению. Волновой пакет можно определить тремя параметрами: частотой, масштабом и положением. Временное положение может быть вычислено как центр масс ,частота – центр масс спектра  волнового пакета. Масштаб характеризует ширину  или неопределенность временного положения. Этот параметр, по принципу неопределенности,  связан с неопределенностью по частоте: при увеличении неопределенности временного положения, неопределенность по частоте.

Пусть - некоторая функция, определим для нее операции модуляции, расширения и переноса следующим образом:

, , .

Набор полученных с помощью данных операций расширенных, перенесенных и модулированных , формирует семейство волновых пакетов с параметрами f, s, p.

Компонента функции с параметрами f, s, p можно вычислить как скалярное произведение на волновой пакет с такими же параметрами. Если эта величина большая, можно считать, что энергия функции сконцентрирована в масштабе s вблизи частоты f и положения p.

Вейвлетные пакеты

Новый класс ортонормальных базисов можно получить, создав «библиотеку» модулированных колебаний, из которой можно извлечь различные базисы, например функции Уолша, вейвлетные базисы. Отличительной особенностью этих новых функций, по сравнению с волновыми пакетами, является свойство ортогональности.

Пусть  и  - импульсные характеристики некоторых фильтров, со спектрами

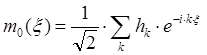
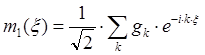                                                              (1)

соответственно. Эти фильтры называются квадратурными зеркальными фильтрами, если следующая матрица является унитарной:

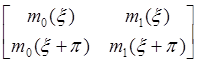.                                                              (2)

Условие для квадратурных зеркальных фильтров можно записать в таком виде

,                                                (3)

где l – длина фильтров, - символ Кронекера.

Введем операции  и  над отсчетами

.                                                                 (4)

которые соответствуют прохождению отсчетов  через фильтры h и g и последующее прореживание отсчетов.

Эти операции имеют сопряженные

.                                                                  (5)

Они соответствуют добавлению между отсчетами сигнала нулевых отсчетов о последующее прохождение полученного сигнала через фильтры с обратной импульсной характеристикой.

Преобразование - ортогональное и для него выполняется соотношение

                                                                                   (5.1)

Вейвлетные пакеты с фиксированным масштабом.

Определим рекурсивно следующую последовательность функций

                                                        (6)

Можно доказать, что функции , для целых  и ,  формируют ортонормированный базис. Пространство, образуемое функциями , будем обозначать .

Перепишем формулы (6) в следующем виде

.     (7)

Здесь выражение  понимается как последовательность по j  при t и n фиксированных.

Используя (5.1) можно получить

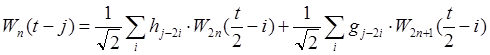    (8)

В случае

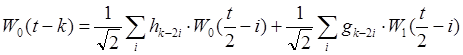           (9)

На основе этой формулы можно представить разложение функции  в пространстве в виде  пары рядов

                            

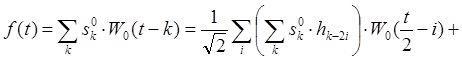
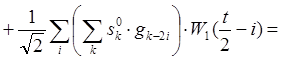
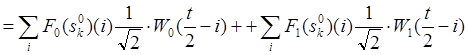          (10)  

В более общем случае, если определенно разложение функции в пространстве

                                                                                    (11)

то можно записать

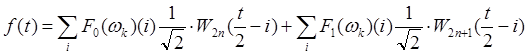  или    , где  и .                                              (12)

Введем оператор масштабирования в таком виде  .

Равенство (12) показывает, что

 или       

,

,

, в общем случае

.

Набор функций  образует так называемый вейвлетный пакет, аналогичный функциям Уолша. Если использовать фильтры с импульсными характеристиками 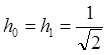, , 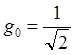 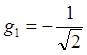и рассматривать функции на интервале , то - функции Уолша в упорядочивании Пейли.

Общие вейвлетные пакеты.

Все функции , рассмотренные выше, имели одинаковый масштаб. Но возможно разложение в базисе со смешанным масштабом. Из (12) видно, что

или в общем случае . Это позволяет упростить разложение в пространстве , применяя масштабирование. Для этого можно использовать следующую теорему:

Для любого разбиения неотрицательных целых , набор

функций является ортонормальным   базисом.

Базисом вейвлетных пакетов называется любой ортонормированный базис, выбранный из функций .

Теперь, наряду с уже рассмотренными базисами, все функции в которых имели одинаковый масштаб (например, функции Уолша), можно ввести и такой базис          .

Дискретные вейвлетные пакеты.

Пусть  - исследуемая функция. Её коэффициенты разложения в пространстве  можно определить так