Радиопеленгационное устройство инструктора парашютной туристической группы для полярных условий, страница 17

Многолетний опыт парашютных прыжков показывает, что при десантировании опытных парашютистов закон распределения расстояний бизок к нормальному с очень небольшой дисперсией, в то время как при выброске неопытных парашютистов  разнос весьма значителен ( при прыжках с высоты  1000 метров разнос можент быть до 10 км), и закон распределения близок к равновероятному.

Второй случай характерен для наших условий. Плотность распределения вероятностей расстояний описывается выражением :

W(r)=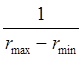 , при r_min  £ r£ r_max.

Математическое ожидание :

M_r = 0,5(r_min +r_max).

В рассматриваемых условиях  r_min=100 м, r_max= 10 км. Математическое ожидание составит 5050 м.

Плотность вероятности распределения распределения напряжения сигнала в точке приема можно определть следующим образом :

W(U_c) = W(r = f(U_c));

Вероятность того, что уровень сигнала в точке приема окажется меньше порога чувствительности приемника можно определить так :

Р( U_c < Е_А ) =  ;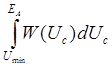

Ранее упоминалось, что напряженность поля над диэлектрической поверхностью описывается квадратичной формулой         Введенского. Тогда напряжение сигнала в приемнике будет описываться следующим выражением :

U_c = ;

где h_д - дейчствующая высота антенны.

После несложных преобразований можно получить выражение для вероятности достверного приема :

Р( U_c >Е_А )   = 1- Р( U_c < Е_А )= 1- ;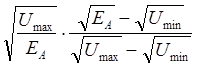

Р( U_c >Е_А )   = 1- ;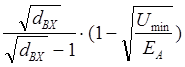

где d_вх  - динамический диапазон сигналов по напряжению на входе приемника, выраженный в относительных единицах.

Ранее было показано, что динамический диапазон D_вх = 80 дБ, что соответствует d_вх»× 10⁴.

Указанное выражение учитывает лишь изменения уровня сигнала от расстояний. Следует также учитывать возможное  затенение радиотрассы случайными препятствиями и линией горизонта.

Вероятность того, что расстояние между приемником и передатчиком не превышает расстояния прямой видимости r₀  описывается выражением :

P(r < r₀) ==.

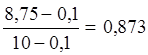Вероятность отсутствия превышения слчайного рельефа  над случайным уровнем первой зоны Френеля зависит от закона распределения высот рельефа. Для равновероятного закона распределения  высот рельефа данная вероятность определяется следующим образом  [10] :

P(h < b₁)=  ;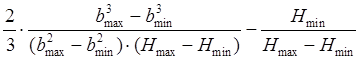

где H_max - наибольшая высота препятствия;

H_min -   наименьшая высота препятствия;

b₁ -  радиус первой зоны Френеля.

b₁ = .

Ориентировочно  принимаем H_max= 2м, H_min=10 км. Подставляя числовые данные в приведенное выражение находим :

P(h < b₁) = 0,998 .

Полная вероятность достоверности приема , то есть вероятность того, что уровень сигнала  на входе приемника превышает уровень чувствительности определяется произведением трех указанных вероятностей, поскольку события, описываемые ими являются независимыми.

          P₀ = Р( U_c >Е_А )P(r < r₀)P(h < b₁).

Задаваясь значением полной вероятности достоверности приема можно получить соотношение между необходимой мощностью передатчика и чувствительностю приемника :

;

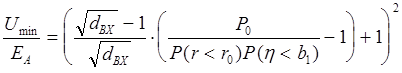U_min - действующее значение минимального сигнала на входе.

U_min =;

где P_min  - мощность минимального сигнала на входе приемника ;

R_вх -   входное  сопротиввление приемника.

P_min = Р _перG₁G₂h₁h₂L_max ;

где Р _пер - мощность излучения передатчика ;

G₁ - коэффициент усиления передающей антенны ;

G₂ - коэффициент усиления приемной антенны ;

h₁ - к.п.д. передющей антенны ;

h₂ - к.п.д. приемной антенны и фидерного тракта .

L_max - максимальное затухание мощности радиоволн на радиотрассе.

Таким образом получаем связь чувствительности приемника и мощности передатчика при заданной вероятности достоверного приема :

Е_А  =  .

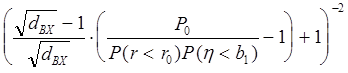Подставляя  числовые  значения R_вх  = 50 Ом, h_{1 =}h_{2 =} 0,9, L_max= -145,5 дБ (6,3 *10^-15), G₁ = 1,64, G₂ = 2,5,  d_вх = 2,317× 10⁴, P(r < r₀) = 0, 873 , P(h < b₁) = 0,998, P₀ = 0,999   получим :

E_A = 0,96 , мкВ

При  мощности излучения передатчика  2,2 Вт необходимо иметь чувствительность приемника для обеспечения требуемой вероятности достоверности приема  Е_А =1,4 мкВ.