Для прогнозирования издержек сырья используем динамические ряды, которые показывают их изменения по периодам. В зависимости от исходных данных (табл. 2.1.) в качестве главных уравнений могут быть выбраны различные типы кривых (степенная зависимость, показательная зависимость и гиперболическая зависимость) или прямой линии.
Таблица 2.1.
Исходные данные по прибыли
(И ГДЕ «ИСХОДНЫЕ ДАННЫЕ ПО ПРИБЫЛИ?»
|
Периоды |
Уровень издержек обращения, в % к прибыли |
|
2000 |
87,7 |
|
2001 |
83,7 |
|
2002 |
81,5 |
|
2003 |
86,7 |
|
2004 |
81,2 |
Сущность экономико - математического метода заключается в определении коэффициентов сравнения факторных (Х) и результативных (У) признаков, путем соотношения значений к минимальному или максимальному уровню.
Чтобы определить вид уравнения, необходимо построить график по отчетным данным (динамическим рядам). По данным таблице 2.1. строим точечный график динамики изменения издержек обращения в процентах к прибыли за период 2000-2004 гг. (рис.2.1.). В ЭТОЙ ТАБЛИЦЕ НЕТ ТАКИХ ДАННЫХ
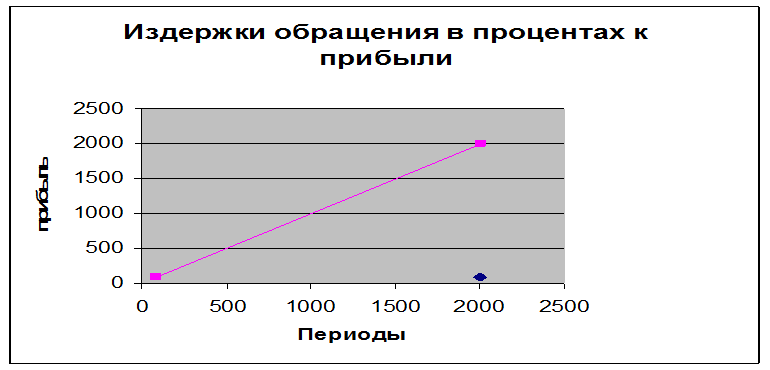
Рис. 2.1 Издержки обращения в процентах к прибыли ГДЕ?
Из рисунка 2.1. видна тенденция изменения издержек обращения в процентах к прибыли, она идет по прямой линии, т.е. с каждым годам прибыль увеличивается.
Зависимость можно описать линейным уравнением. В связи с этим факторный и результативный признак Х и У увеличивается.
Между факторами существует прямая связь.
Построим линейное уравнение:
У = ВХ + А, где:
У – прибыль;
Х - период;
В – ежегодный прирост;
А – издержки при нулевом периоде (Х=0). А И В – ЧИСЛА КОКРЕТНЫЕ, КОТРЫЕ МЫ ИЩЕМ, ЧТОБ ИХ УЗНАТЬ МОДЕЛЬ СТРОИМ, ВСЕ РАСЧЕТЫ ПРОВОДИМ. ХОТЯ, ДЕЙСТВИТЕЛЬНО, ПРИ Х=О – МАТЕМАТИЧЕСКИ А=ИЗДЕРЖКАМ (ЕСЛИ Х=ИЗДЕРЖКИ)
Расчеты этих параметров сведены в табл.2.4. Из столбца «коэффициенты» полученные результаты подставляем в уравнение, которое имеет вид:
У = -1 Х + 2086,16. (ПОСЛЕ ТАБЛИЦЫ И ПИШИТЕ УРАВНЕНИЕ)
В табл. 2.5., фактическое t-статистическое равно 1,14, что свидетельствует о правильности произведенных вычислений, так как табличное (минимальное значение) равно 1. В нашем случае связь прямая.
Таблица 2.2
Вывод итогов регрессионной статистики
|
Регрессионная статистика |
|
|
Множественный R |
0,534278 |
|
R-квадрат |
0,285453 |
|
Нормированный R-квадрат |
0,047271 |
|
Стандартная ошибка |
2,888598 |
|
Наблюдения |
5 |
Показатель R-Square показывает в скольких процентных случаях уравнение дает правильный результат анализа и прогноза. R-Square = 28%, это означает, что модель дает правильный результат в 28% случаев и имеет смысл ее дальнейшего построения. В таблице 2.2. показан расчет R-квадрата, он равен 0,285453. Этот коэффициент показывает тесноту связи эмпирических и теоретических уравнений.
Таблица 2.3.
Дисперсионный анализ
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
1 |
10 |
10 |
1,198466 |
0,35365 |
|
Остаток |
3 |
25,032 |
8,344 |
||
|
Итого |
4 |
35,032 |
Экономическую модель необходимо оценить по F критерию Фишера.
В нашем случае F = 1,2, полученный F сопоставляем с табличными данными для определения существенности и несущественности детерминации. Табличное значение зависит от степени свободы, где к1 – это количество Х в модели. к2 – количество наблюдений за минусом количество Х, т.е. независимых факторов. к1=1, к2=4. Табличное значение будет равно 7,71, это говорит о том, что модель фактически пригодна и удовлетворяет F пригодности.
Таблица 2.4.
Статистика по критерию Стьюдента.
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
|
Y-пересечение |
2086,16 |
1828,737 |
1,140765 |
0,336788 |
-3733,7 |
7906,018 |
-3733,7 |
7906,018 |
|
Переменная X 1 |
-1 |
0,913455 |
-1,09474 |
0,35365 |
-3,90702 |
1,907021 |
-3,90702 |
1,907021 |
Проводим следующий этап анализа экономико – математической модели, проверку модели Т - статистики по критерию Стьюдента.
Данный критерий зависит от степени свободы к2.
Табличное, т.е. критическое значение равняется 1.
Фактическое значение в нашем примере больше, чем табличное. Значит связь между значениями тесная и построенная модель может быть пригодна при анализе и прогнозировании значения показателя прибыли в зависимости от динамики численности работников. табличное т.е. .и.- математической том, что модель фактически пригодна и удовлетворяет строение было бы целесообразно.
Результаты расчетов показывают, что связь между показателями прибыли по периодам прямопропорциональная, линейная, она обладает высокой устойчивостью.
Рассмотрим прогноз увеличения прибыли в таблице 2.5. за 2005-2007 года.
Таблица 2.5.
Исходные данные по прибыли АНАЛОГИЧНО
|
Периоды |
Издержки обращения в % к прибыли |
|
2005 |
88,8 |
|
2006 |
89,0 |
|
2007 |
92,0 |
|
Итого: |
269,80 |
Проведя расчеты, мы можем с уверенность сказать, что внедрение контроллинга с 2000 года принес предприятию питания существенный экономический рост. Результат исследования экономико-математической модели свидетельствует, что прибыль в периоде 2000-20004 гг., возрастает ежегодно, перспектива увеличения издержек обращения в процентах к росту прибыли составляет 92% на 2007 год.
Спрогнозировав увеличения издержек обращения в процентах к прибыли на 2007 год, мы можем сказать, что рост контроллинга предприятия питания будет возрастать.
Спрос на контроллинг рождает каждый год новые методы, инструменты управления, более эффективные и учитывающие внешние факторы потребительского рынка, воздействующие на статьи расходов и доходов предприятия питания.
ЗДЕСЬ ВСЕ ПЕРЕПУТАНО – НАПРОЧЬ.
ЛУЧШЕ ОСТАВЛЯЙТЕ ПРЕДЫДУЩУЮ МОДЕЛЬ (С ЦИФРАМИ В УРАВНЕНИИ).
КАК МОЖНО НА ГРФИКЕ ОДНИ ПОКАЗАТЕЛИ НАПИСАТЬ, В ТАБЛИЦЕ ДРУГИЕ, В ТЕКСТЕ – СКАЗАТЬ, ЧТО АНАЛИЗИРУЕМ ЕЩЕ ККУЮ-ТО ЗАВИСИМОСТЬ?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.