Тепломассообмен. Основные законы и механизмы переноса теплоты, импульса и вещества в материальной среде. Теплопроводность: температурное поле; гипотеза Био-Фурье; краевая задача и условия однозначности; частные случаи теплопроводности; стационарный теплообмен, страница 3

б) дифференциальное уравнение теплопроводности для трёхмерного стационарного течения:

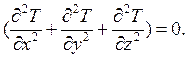                                                                                                                                                                                                                                                                     (5)

            Для стационарного температурного поля распределение температуры в теле не зависит от физических свойств самого тела. В нестационарном поле физические свойства тела влияют через коэффициент температуропроводности а.

            Итак, физический смысл дифференциального уравнения теплопроводности: оно устанавливает связь между временным и пространственным изменением (распределением) температуры в любой точке тела, в которой происходит процесс теплопроводности.

            При конкретном рассмотрении задачи необходимо в дифференциальное уравнение теплопроводности добавить математическое описание частных особенностей процесса.

            При математической постановке задачи необходимо учитывать:

– геометрическую форму тела;

– физические свойства;

– задать краевые условия: начальные и граничные условия.

            Начальные условия необходимы при рассмотрении нестационарных  процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени

            Граничные условия:

– I-го рода: задаётся распределение температуры на поверхности тела для каждого момента  времени:  в частном случае

– II-го рода: задаются значения теплового потока для каждой точки поверхности тела и любого момента времени:в частном случае

– III-го рода: задаётся температура окружающей среды  и закон теплообмена между поверхностью тела и окружающей средой: закон Ньютона-Рихмана.             

            Если использовать закон Фурье, то (45) будет иметь вид:

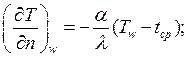
– IV-го рода (условия совместности): равенство тепловых потоков на границе соприкосновения тел:

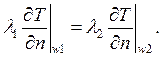                                                                                                                                                                                                                         (6)

            Перечисленные геометрические и физические особенности тела, а так же краевые условия определяют условия неоднозначности (единственности). Задачи, решаемые с их помощью, называются краевыми.

            При решении конкретной задачи используют только одно из граничных условий.

            Теплообмен и теплопроводность широко распространены.

            Рассмотрим частные случаи теплопроводности:

            1) Стационарная теплопроводность:

            а) трехмерная задача:

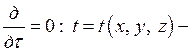            функция координат и времени; условие стационарности теплообмена всегда предполагает наличие постоянно действующего источника (стока) тепла. Чаще всего источников нет.

            основное уравнение в трехмерной задаче;

            б) двухмерная задача (без источников тепла):

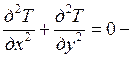            плоская задача на поверхности;  По одной из координат температура изменяется крайне мало (распространенное тепло по стержню);

            в) одномерная задача, имеющая практическое значение – это задача о переносе тепла через плоскую однослойную однородную стенку:

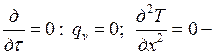            температурное поле стационарное и температура изменяется по одной координате.

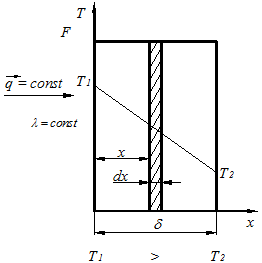            Запишем выражение для теплового потока через однослойную однородную плоскую стенку:                    

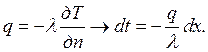                                                               (7)

            Возьмём интеграл от (6):

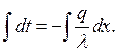
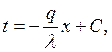
где постоянная интегрирования.

            определяется из таких условий:

        1) при

Рисунок 2.3 – Схема теплового потока        через плоскую однослойную однородную стенку

                                                                                                                                                        2) при                                                                   

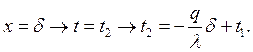
            Тогда из (7) следует закон Фурье в интегральной форме:

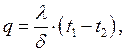
где 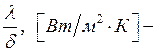тепловая проводимость стенки;                                                                                                                                                                 

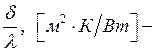      термическое сопротивление стенки.                                                                                                                             

            При  температура внутри стенки изменяется по прямой линии.

            Полный тепловой поток:

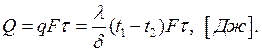
             связаны между собой и, зная три величины, можно найти четвёртую:

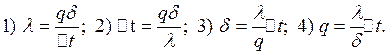
3. Стационарная теплопроводность многослойной плоской стенки (граничные условия первого рода). Термическое сопротивление.

            Рассмотрим задачу о переносе тепла через многослойную плоскую неоднородную стенку.

            Стенки, состоящие из нескольких разнородных слоев, называются многослойными.

            Например, стенки домов, теплоизоляция паровых котлов.

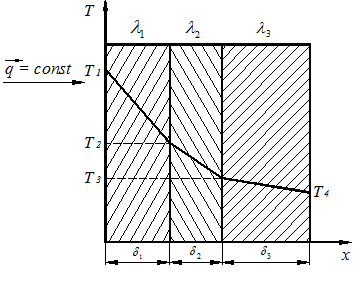
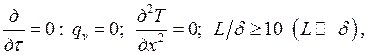
где длина (высота) стенки;

       толщина стенки.

            Граничные условия:

температуры на границе слоев.

            Термическим контактным сопротивлением пренебрегаем (пластины являются абсолютно гладкими).

Рисунок 3.1 – Схема теплового потока        через плоскую многослойную стенку

            При стационарном режиме теплообмена

            На основе 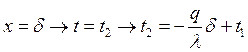 плотность теплового потока через стенку для каждого слоя:

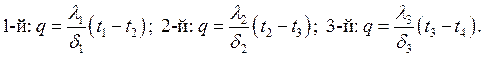
            Из выражения для полного теплового потока: 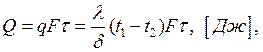 следует:

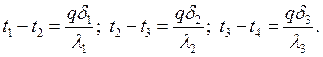                                                                                                                                                                                                 (1)