В условиях нестационарности температурное поле представляется в виде сменяющихся во времени картин изотермических линий или поверхностей, причём каждая из картин является отображением мгновенного температурного поля.
Согласно гипотезе
Фурье максимальная плотность теплового потока через выделенную элементарную
площадку ![]() на изотерме будет направлена
перпендикулярно к ней и прямопропорциональна градиенту температуры,
характеризующего интенсивность изменения температуры:
на изотерме будет направлена
перпендикулярно к ней и прямопропорциональна градиенту температуры,
характеризующего интенсивность изменения температуры:
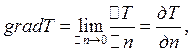
где ![]() расстояние
между изотермическими поверхностями.
расстояние
между изотермическими поверхностями.
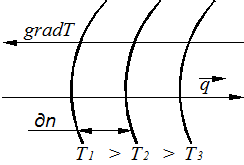
Интенсивность изменения температуры может быть охарактеризована плотностью изотерм на некотором линейном отрезке.
В процессе
теплопроводности количество переданного тепла ![]() пропорционально
температурному градиенту и площади
пропорционально
температурному градиенту и площади
Рисунок 2.1 – Схема процесса кондукции сечения, перпендикулярного направлению распространения тепла – закон Фурье:
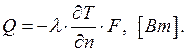
Математическое выражение основного закона распространения тепла теплопроводностью (закон Фурье):
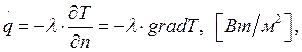
где![]() коэффициент
теплопроводности – физический параметр вещества и характеризует способность
тела или среды проводить тепло. Он определяет количество тепла, которое
проходит в единицу времени через 1 м2 поверхности при изменении
температуры на
коэффициент
теплопроводности – физический параметр вещества и характеризует способность
тела или среды проводить тепло. Он определяет количество тепла, которое
проходит в единицу времени через 1 м2 поверхности при изменении
температуры на ![]() на 1 м «пути» теплового потока.
на 1 м «пути» теплового потока.
Градиент температуры – вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и числено равный производной от температуры по этому направлению.
Краевой задачей называется математическая модель теплопроводности для описания температурного поля. Эта модель включает дифференциальные уравнения теплопроводности совместно с условиями однозначности (краевые условия).
В основу вывода дифференциального
уравнения теплопроводности (уравнение Фурье-Кирхгофа) положены возможность
локального термодинамического равновесия для любой макроскопической точки тела
и закон сохранения энергии:![]() количество тепла
количество тепла ![]() , введённое в элементарный объём из
вне за время
, введённое в элементарный объём из
вне за время ![]() вследствие теплопроводности, а также
от внутренних источников, равно изменению внутренней энергии вещества:
вследствие теплопроводности, а также
от внутренних источников, равно изменению внутренней энергии вещества:
![]()
где![]() количество
тепла, введённое в элементарный объём за время
количество
тепла, введённое в элементарный объём за время ![]()
![]() количество тепла, которое выделилось в элементарном
объёме за счёт внутренних
количество тепла, которое выделилось в элементарном
объёме за счёт внутренних
источников за
время ![]()
![]() изменение внутренней энергии.
изменение внутренней энергии.
Рассмотрим случай
одномерного нестационарного температурного поля ![]() а
так же
а
так же ![]() или
или ![]()
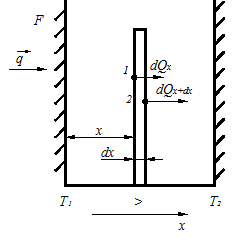 Где
Где ![]()
![]() толщина
элементарного слоя;
толщина
элементарного слоя; ![]() площадь;
площадь;
![]() время
время
![]()
![]() коэффициент
теплопроводности.
коэффициент
теплопроводности.
1) Тепловой поток (количество тепла), входящий в т. 1:
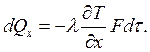
2) Количество тепла, выходящее из т. 2:
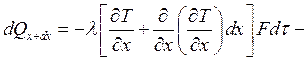 превышение.
превышение.
![]() так как
так как ![]()
|
3) Возьмём разность:
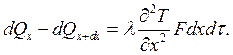 (1)
(1)
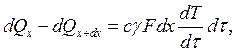 (2)
(2)
где ![]() теплоёмкость;
теплоёмкость;
![]() удельный вес или
удельный вес или![]() плотность вещества
плотность вещества ![]()
![]() объём.
объём.
4) Приравняв (1) и
(2) и, сократив их на ![]() получим:
получим:
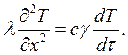
5) Изменение температуры в слое для одномерного нестационарного течения:
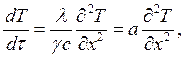 (3)
(3)
где 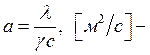 коэффициент
температуропроводности, характеризующий темп нагревания или охлаждения
тела.
коэффициент
температуропроводности, характеризующий темп нагревания или охлаждения
тела.
Величина обратная ![]()
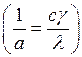 называется
тепловой инерцией тела.
Формула (3) представляет собой арифметическое
выражение дифференциального уравнения теплопроводности для одномерного
нестационарного течения.
называется
тепловой инерцией тела.
Формула (3) представляет собой арифметическое
выражение дифференциального уравнения теплопроводности для одномерного
нестационарного течения.
6) Для трёхмерного нестационарного течения уравнение (3) имеет вид:
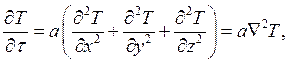 (4)
(4)
где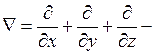 оператор Лапласа.
оператор Лапласа.
Решение уравнения (4) обладает свойствами суперпозиции, аналогично решению обыкновенного однородного дифференциального уравнения 2-го порядка. Общее решение такого уравнения является суммой частных решений.
В соответствии с правилом суперпозиции:
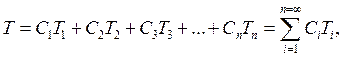
где![]() константы.
константы.
При наличии внешних источников тепла (тепловыделительные источники тепла ядерных реакторов ТВЭЛ; проводник, который омывается воздухом) дифференциальное уравнение теплопроводности для трёхмерного нестационарного переноса тепла будет иметь вид:
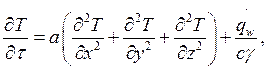
где ![]() общая
производительность внутренних источников тепла.
общая
производительность внутренних источников тепла.
7) Рассмотрим два случая:
а) если температурное поле стационарное,
то ![]() . Тогда дифференциальное уравнение
теплопроводности для одномерного стационарного течения будет иметь вид:
. Тогда дифференциальное уравнение
теплопроводности для одномерного стационарного течения будет иметь вид:
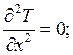
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.