Министерство Образования Республики Дагестан
“Шаг в будущее”
 |
"Решение некоторых видов уравнений
при помощи неравенств"
Автор: ученик 11б класса РМЛ
Сулейманов Фарид
Научный руководитель: учитель математики РМЛ
– Махачкала 2002 –
РЕШЕНИЕ НЕКОТОРЫХ ВИДОВ УРАВНЕНИЙ ПРИ ПОМОЩИ НЕРАВЕНСТВ
В школьном курсе математики часто используют четыре основных метода решения уравнений: разложение на множители, замена переменной, переход от равенства функций к равенству аргументов, функционально-графический. Кроме перечисленных методов существуют и специальные. Они используются в том случае, когда уравнение громоздко решается основными методами. Рассмотрим один из специальных методов решения - решение уравнений с помощью неравенств. Этот метод рассмотрим на примерах.
Применение неравенства Коши
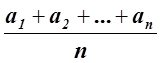
![]()
![]() ,
,
известное как неравенство Коши.
Его можно переписать следующим образом:
a1 + a2 + ... + an ![]() n
n![]() .
.
Рассмотрим
частный случай неравенства Коши для n = 2,
т.е. 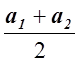
![]()
![]() , или a1 + a2
, или a1 + a2 ![]() 2
2![]() .
.
a1
+ a2
![]() 2
2![]() ,
,
a1
+ a2
– 2![]()
![]() 0,
0,
(![]() )2
)2![]() 0.
0.
Отсюда следует, что (![]() )2
= 0, если a1 = a2. Итак, при a1 = a2 в неравенстве
Коши достигается равенство. Для всех других значенийn условиеa1 = a2 = … =an также обеспечивает обращение неравенства Коши в
равенство.
)2
= 0, если a1 = a2. Итак, при a1 = a2 в неравенстве
Коши достигается равенство. Для всех других значенийn условиеa1 = a2 = … =an также обеспечивает обращение неравенства Коши в
равенство.
Приведем примеры:
1.
Решить уравнение: ![]() = 4x+
= 4x+![]() .
.
Р е ш е н и е.
Область определения неизвестного:x![]() R,
x
R,
x![]() 0.
0.
К левой части применим неравенство Коши дляn = 3. Но неравенство Коши выполняется для неотрицательных членов (множителей). Левая и правая части уравнения являются нечетными функциями. Тогда корни уравнения числа противоположные, поэтому решить уравнение для x>0. Преобразуем уравнение, умножив обе его части наx, так как x >0.
x ![]() = 4x2+4
= 4x2+4![]()
![]() =
4x2+4.
=
4x2+4.
Рассмотрим левую часть и оценим ее:
![]() =
= ![]()
![]()
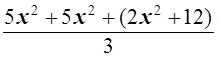 =
=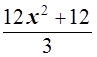 ,
,
т.е. ![]()
![]() 4x2+4, а по условию
4x2+4, а по условию ![]() = 4x2+4. Таким образом
неравенство Коши обращается в равенство. Это возможно, если
= 4x2+4. Таким образом
неравенство Коши обращается в равенство. Это возможно, если ![]()
или
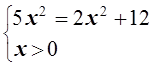
![]() x= 2
x= 2
Учитывая нечетность функций, входящих в уравнение, получаемx= ± 2.
О т в е т: x= ± 2.
1.2
Решить уравнение: 4x![]() =
39x2+16.
=
39x2+16.
Р е ш е н и е. Область определения неизвестного:x![]() R,
x > 0.
R,
x > 0.
К левой части применим неравенство Коши дляn = 4. Но неравенство Коши выполняется для неотрицательных членов (множителей).
4x ![]() = 39x2+16
= 39x2+16 ![]()
![]() = 39x2+16.
= 39x2+16.
Рассмотрим левую часть и оценим ее:
![]() =
= ![]()
![]()
![]()
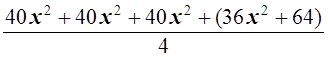 =
=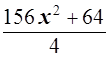 , т.е.
, т.е.![]()
![]()
![]() , а по условию
, а по условию ![]() =
=![]() . Таким
образом неравенство Коши обращается в равенство. Это возможно, если
. Таким
образом неравенство Коши обращается в равенство. Это возможно, если ![]()
или
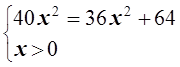
![]() x= 4
x= 4
О т в е т: x= 4.
1.3
Решить уравнение: x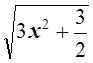 =
2x2
+
=
2x2
+ ![]() .
.
Р е ш е н и е. Область определения неизвестного:x![]() R,
x > 0.
R,
x > 0.
К левой части применим неравенство Коши дляn = 2. Но неравенство Коши выполняется для неотрицательных членов (множителей).
x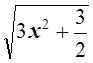 = 2x2 +
= 2x2 + ![]()
![]()
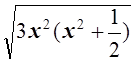 =
2x2
+
=
2x2
+ ![]() .
.
Рассмотрим левую часть и оценим ее:
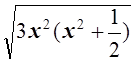
![]()
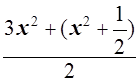 =
=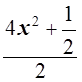 , т.е.
, т.е. 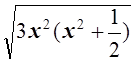
![]() 2x2+
2x2+ ![]() , а по условию
, а по условию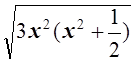 = 2x2+
= 2x2+ ![]() . Таким образом неравенство Коши обращается
в равенство. Это возможно, если
. Таким образом неравенство Коши обращается
в равенство. Это возможно, если 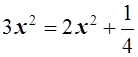
или
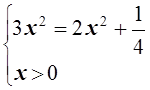
![]() x=
x= ![]()
О т в е т: x= ![]() .
.
2. Решить уравнение: 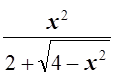 +
+
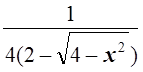 = 1.
= 1.
Р е ш е н и е. Видно, что левая часть уравнения представляет собой функцию, которая
определена при условиях ![]()
![]() 0 и
0 и ![]()
![]() 2. Отсюда x
2. Отсюда x ![]() [-2;0)
[-2;0) ![]() (0; 2].
(0; 2].
Пусть ![]() = y, y
= y, y ![]() 0. Тогда
0. Тогда ![]() = y2
= y2 ![]() x2 = 4 – y2. С
учетом обозначения исходное уравнение примет вид:
x2 = 4 – y2. С
учетом обозначения исходное уравнение примет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.