Тема: «Комплексные числа»
П.3. Комплексная плоскость
Рассмотрим плоскость прямоугольной системой координат Оху. Каждому комплексному числу z=x+iy может быть сопоставлена в соответствии точки плоскости z(x,y), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, наз. комплексной плоскостью.
На Ох расположены действительные числа z=x+oi=x, поэтому Ох – действительная ось; на Оу расположены число мнимые числа z=o+iy=iy, поэтому Оу – мнимая ось.
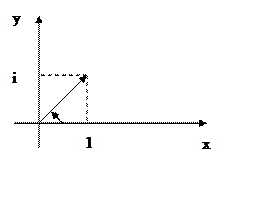
Заметим, что r=/z/ - расстояние т. z от
начала координат. С каждой точкой z связан радиус – вектор этой точки Оz; угол, образованный радиус-вектором Оz с осью Ох, называется
аргументом φ=Аrg z этой точки. Здесь – r<Arg z < +
(Для точки z=0 arg-
). Наименьшее модулю значение Arg z называется главным значением и обозначается arg z П <arg z< П.
Рис.: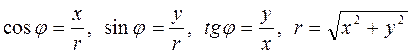 
Примеры: 1) z=2, z=2, arg2=0;
2) z=-1; z=1, arg(-1)=П;
3) z=I; z=1, arg=
Модуль r и arg z комплексные число z можно рассмотреть как координаты т.z/
x=z cos φ, y=r sin φ.
То получили тригонометрическую форму комплексного числа:
z=x+iy = r cosφ + i r sinφ = r (cosφ + I sinφ)/
Чтобы сложить (выч.) два компл. числа в тригонометрической форме и сложить (выч.) их радиусы-векторы (по правилу параллелограмм).
Теорема 1.
Модуль произведения к.r. равен произведению модулей, а аргумент равен сумме аргументов множителей.
Умножение и деление чисел в тригонометрической форме.
Следствие.
Модуль целой положительной степени к.r. равен такой же степени модуля α argzn=argz т.е.
argzn = nargz т.е.
zn = zn (coshφ+isinhφ) – формула Муавра (Абрахам Муавр 1667-1754 английский математик).
Теорема 2.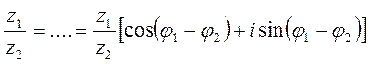 
z2≠0
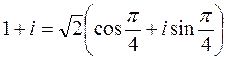
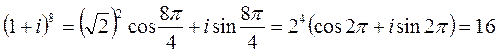
Извлечение корня из компл.числа
Пусть 
т.е. уже извл. ст. из к.z. z=r(cosφ+isinφ). Тогда **** т.1 (1) возв. в степ. h.
Отсюда 
Таким образом 
(понимает арифметическое значение корня)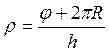 
.
Получили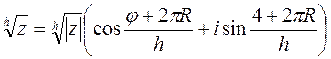 
(R=0, 1, 2, 3, …, n-1)
Корень n-й степени из 
к.r. z≠0 имеет точно n значение.
Пример 1.
z=-1+i Найти 
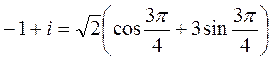
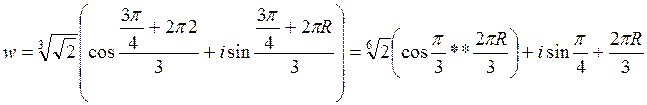R=0,1,2
Отсюда
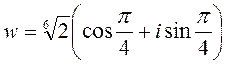
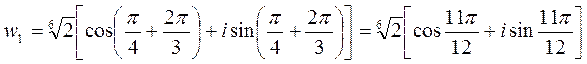
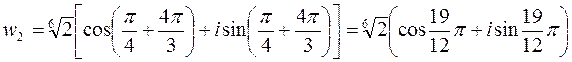
Точки w0, w11, w2 представляют собой равноотстоящие друг от друга точки
расположенные по окружности радиуса 
Пример 2.
Схеме
?
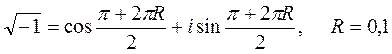
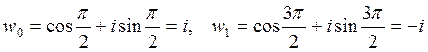
0 1 0 -1
т.к. 
формула Эйлера
Тема: «Комплексное число»
П.1. Определение комплексного числа и арифметические действия над ними.
Опр. 1. Комплексным числом называется выражение вида
(1) z=x+iy или z=x+yi, [компл. чисел] где х и у действительные
числа, I – линейная единица: 
Действительные числа ч и у наз. соответственно действенной и мнимой частями числа z и обозначаются и образом: х=Rеz, y=Imz
Например, z=5+2i – комплексное число, Rеz=1,2, Imz=-0,7
Опр.2 Число z=x+i(-y)=x-iy называется сопряженным числу z=x+iy
Например, для числа ž=6+2i число z=6-2i сопряженное.
Числа z=-1,7-3i и ž=-1,7+3i сопряженное
Очевидно, что Rež = Rez, Imž = -Imz
Опр. 3. Модулем
комплексного числа z называется
неотрицательное число 
Очевидно, что |ž| = |z|.
Множество комплексных чисел обозначается С.
На множестве комплексных чисел определено равенство двух чисел, операции сложения, вычитание, умножение и деление:
Пусть z1=x1+iy, z2=x2+iy2 – комплексное число
1) z1=z2 <=> Re z1=Re z2, Im z1=Im z2.
z=0 <=> Re z=0, Im z=0
Числа вида x+i0=x действительные числа
Числа вида 0+iy=iy – чисто мнимые
z1+z2=(Re z1±Re z2) + (Im z1±Im z2)
2) z1±z2 = (x1+y1i) ± (x2+y2i) = (x1±x2) + (y1±y2)i т.е. чтобы сложить (вычесть) два комплексных числа нужно сложить (вычесть) действительные части, сложить (вычесть) мнимые части (полученные действия и мнимые части записать в виде суммы).
Пример z1=2+3i, z2=7-11i
z1±z2 = (2+3i) + (7-11i) = 2+3i+7+(-11)i=(2+7)+(3+(-11))i=9+(-1)i=9-4i;
z1-z2 = (2-7) + (3-(-11))i=-5+14i
3) z1·z2 = (x1+y1i) ± (x2+y2i) = x1x2 + x1y2 = x1x2 + x1y2i+x2y2i – y1y2 = (x1x2 + x1y2) + (x1y2 + x2y1)i.
y1i·y2i = y1·y2·i2
Пример. z1=2+3i z2=7-11i z1·z2=(2·7-3+..)+(2(-11)+7·3)I = 47-1i
Очевидно, что z1·ž = |z|2 = x2+y2
4) 
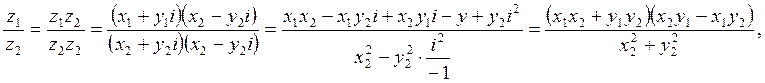
z2 ≠ 0
Пример z1=1+3i, z2 = 2-i
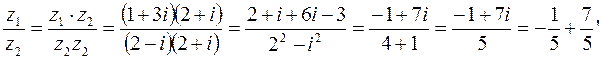
П.2 Комплексная плоскость. Тригонометрическая форма комплексных чисел.
Рассмотрим координатную плоскость Оху. Комплексное число z=x+iy можно изобразить на этой плоскости в виде точки z(x,y). На оси Ох расположены действительные числа, на Оу – чисто мнимые, поэтому Ох – действит. ось, Оу – мнимая ось, плоскости Оху – комплексная плоскость.
Заметим, что |z|=r – расстояние точки z от начала координат, r - радиус-вектор точки z. Радиус-вектор r образует с Ох угол φ. Угол φ=arg z называется аргументом точки z.
Для аргумента φ:
Схема.
(*) 
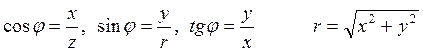
Пример а) z=2, |z|=2, arg z=0, z=-1, |z|=1, arg z =-П
б) z=I, |z|=1, arg z =
из (*) => х=rcosφ, y=isinφ. Также х+iy = rcosφ+irsinφ = r(cosφ+isin), φ=argz.
Выражение вида z=r(cosφ+isinφ) – тригонометрической форме комплексного числа.
Комплексные числа в тригонометрической форме можем складывать, вычитать, умножать, делить.
Пусть z1=r1(cosφ1+isinφ1), z2=z2 (cosφ2+isinφ2)
1) z1+z2 = (|z1|±|z2|)[cos(φ2-φ1)+isin(φ2-φ1)]
Схема
2) z1-z2 = z1-z2 [cos(φ2+φ1)+isin(φ2+φ1)]
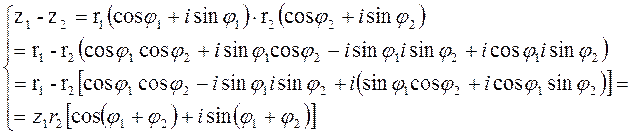
3) zh=|z|h [coshφ+isinhφ]
4) 
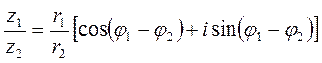
Примеры:
1) (3+5i)(4-i) [17+17i]
2) (6+i)(3-i)
3) Представим числа i, 1+i в тригонометрической форме
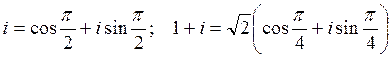|z| =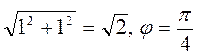 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
