Функции, понятие функции. Определение и возникновение понятия. Лейбниц

Функции

ПОНЯТИЕ ФУНКЦИИ

Представим себе, что автомобиль едет по прямолинейной дороге с постоянной скоростью v. Расстояние s, пройденное им за время t, выражается формулой s = vt. Это прямая пропорциональная зависимость. А вот пример квадратичной зависимости: тело, падающее под действием силы тяжести, проходит путь

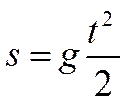
где g — некоторая константа. Или обратно пропорциональная зависимость: связь между давлением р и объёмом Vгаза при постоянной температуре выражается, согласно закону Бойля — Мариотта, формулой/? = c/V. Закон всемирного тяготения устанавливает связь между силой Fвзаимодействия двух тел массы М и m и расстоянием г между ними:

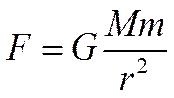
где G— гравитационная постоянная. Здесь мы привели примеры простейших функциональных зависимостей, которые в общем виде можно представить так

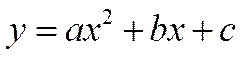
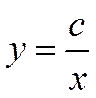
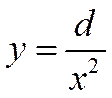
В школе изучают и другие функции: логарифмическую у = log_ax:, показательную = а^х, тригонометрические функции у = sin x;, у = cos x:, у = ctg x: и т. д.

Функция — одно из основных общенаучных понятий; оно выражает взаимосвязь между различными объектами. Понятие функции сложилось не сразу. Вначале оно было расплывчатым и не имело сколько-нибудь отчётливого описания. Первые попытки очертить контуры этого понятия предприняли в конце XVII в. один из родоначальников математического анализа Готфрид Вильгельм Лейбниц, а также его ученики и последователи — братья Иоганн и Якоб Бернулли. Сам термин «функция» принадлежит Лейбницу и происходит от латинского слова functio, что означает «выполнение», «осуществление». Иоганн Бернулли вкладывал в это слово такой смысл: функция — «выражение, составленное каким-то образом из переменной величины и постоянных величин».

Эйлер также понимал под функцией аналитическое выражение, но вместе с тем готов был принять и более широкое толкование: функция — это то, что можно «вычертить карандашом на листе бумаги» (лат. — libera manu

Рис.1.

dicta). Ему были известны случаи, когда функция описывалась словесно или геометрически. Так, функцию у = | х \ (рис. 1) можно определить разными способами, например формулой у = 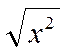(аналитическое выражение). Есть и её геометрическое определение — объединение биссектрис первого и второго квадрантов. Если сказать, что функция у = \х\ принимает значение аргумента, когда аргумент неотрицателен, и равна «минус аргументу», когда аргумент отрицателен, то тем самым будет дано её словесное описание.

Что же предпочесть? Учёные много спорили, было сломано немало копий. Например, Эйлер считал, что класс функций, являющихся «произвольно начерченными кривыми», шире, чем класс функций, задаваемых аналитическими выражениями. Д'Аламбер возражал: получается одно и то же. Даниил Бернулли пошёл ещё дальше: он заявил, что произвольную 2я-пери-одическую функцию можно представить в виде тригонометрического ряда

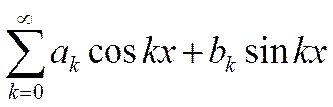
Большинству учёных казалось, что это лишь некоторый узкий класс функций: он уже, чем аналитические выражения, и, разумеется, уже, чем «произвольные кривые».

В начале XIX в. стало выкристаллизовываться понятие функции как соответствия, правила, по которому независимая переменная х из некоего множества Xпреобразуется в переменную у из другого множества У «любым образом» (см. статью «Отображения»). Чтобы лучше освоиться с этой точкой зрения, рассмотрим несколько примеров.

1.  Каждый ученик в школе учится в определённом классе. Если обозначить через Xмножество учеников в данной школе, а через Y—множество классов, то можно сказать, что каждому элементу множества X(т. е. каждому ученику) сопоставлен единственный элемент множества Y(т. е. тот класс, где данный ученик учится).

2.Каждому ученику данного класса в конце года выставляется определённая оценка по математике. Если обозначить через Xмножество учеников в классе, а через F — множество целых чисел от 2 до 5, то можно сказать, что каждому элементу из X сопоставлен единственный элемент из У.

3. Если обозначить через X множество всех действительных чисел