Нестационарная стохастическая модель переменного роста для оценки стоимости некотируемых активов, страница 6

Данные из  строки 2 таблицы представляют предполагаемые прогнозные значения темпов роста дохода в долларах. Темпы роста в рублях получаются из предполагаемых валютных темпов и прогнозируемой инфляции по формуле Фишера:

Окончательный расчет ставок капитализации и дисконта при сделанных предположениях приведен в следующей таблице.

Таблица 21.8

Расчет ставок капитализации и дисконта

Ставки капитализации в строке 3 определяются при помощи уравнения (21.27) с граничным условием (21.30). Рублевые ставки дисконтирования в строке 4 определяются при помощи уравнения (21.31). Валютные ставки дисконтирования в строке 6 определяются из предполагаемых валютных темпов и прогнозируемой инфляции по формуле Фишера

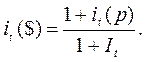
Полученные ставки не являются монотонными по  в силу немонотонности «наведенных» годовых ставок доходности по облигациям и еврооблигациям и, соответственно, немонотонности безрисковых ставок, что свидетельствует о неравновесности рынка эти ценных бумаг. Поэтому в таблице 21.9 приведен расчет ставок для еще одного примера, где искусственно вводятся прогнозируемое монотонное изменение безрисковых ставок и текущей инфляции, чтобы показать, что ставки капитализации и дисконта в этом случае будут также монотонны.

Таблица 21.9

Пример расчета ставок для монотонных исходных данных

В этом примере предполагалось, что:

В заключение отметим, что следует разделять основную модель и ее реализацию для принятого способа экстраполяции бета в прогнозном периоде. В первом случае предполагается только независимость темпов изменения чистого денежного потока, как случайных величин. Во втором случае мы вынуждены были предположить одинаковое распределение соответствующих определенным образом нормированных случайных величин, что несколько снижает общность рассуждений. Тем не менее, исходные рекуррентные уравнения для ставок капитализации и дисконтирования остаются справедливыми в общем случае, имеют фундаментальное значение и могут служить теоретической основой для построения различных процедур, где на входе задаются ожидаемые темпы изменения чистого денежного потока, а на выходе – соответствующие ставки дисконта и капитализации.