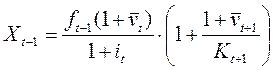Нестационарная стохастическая модель переменного роста для оценки стоимости некотируемых активов, страница 2

.

С учетом (21.9) получим отсюда искомое рекуррентное уравнение для ставки капитализации:

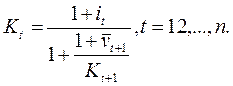                     (21.12)

Граничное условие для уравнения (21.12) дает формула Гордона (21.6):

                          (21.13)

При известных  уравнение (21.12) можно решить последовательно для  отправляясь от граничного условия (21.13).

21.3. Рекуррентное уравнение для ставки дисконта

Согласно основного уравнения модели САРМ, все предположения которой считаются выполненными, справедливо соотношение:

                  (21.14)

где  безрисковая ставка за й период,

 среднее значение случайной доходности  рыночного портфеля за период,

 бета актива, определяемая равенством:

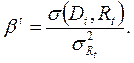               (21.15)

Здесь  ковариация с.в.   среднее квадратическое отклонение с.в.   случайная доходность актива за период t, определяемая равенством

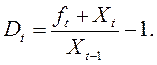
Из (21.9) следует, что

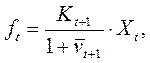
откуда        

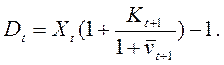                    (21.16)

Подставляя (16) в (15), получим:

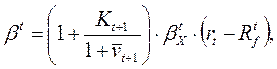
где  бета, определяемая по доходности  актива только за счет изменения стоимости , по формуле

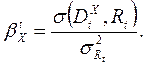
Здесь

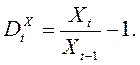
Подставляя (21.17) в (21.15) и (21.14), получим искомое рекуррентное уравнение для

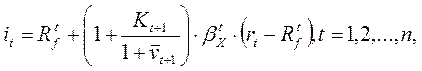              (21.18)

которое следует решать совместно с (21.12) от конца к началу. Причем сначала определяется  по формуле (21.18), а затем  по формуле (21.12) последовательно при

В частности, при  получим из (21.18) равенство

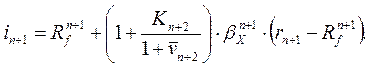
Предполагая, что кроме равенств

 

выполняется равенство

получим отсюда:

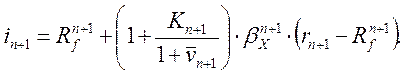           (21.19)

В силу формулы Гордона (21.13), отсюда следует  уравнение для определения неизвестной величины

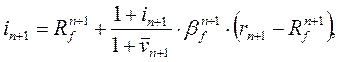
полученное ранее в [5] вместе с формулой для граничного значения

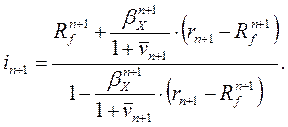                (21.20)

Уравнение (21.18) следует решать, отправляясь от граничного условия (21.20).

21.4. Информационное обеспечение модели

Величины  считаются экстраполяцией соответствующих ретроспективных данных. Величина  экстраполируется по тренду ретроспективных данных. Экстраполяция величин  может быть построена исходя из безрисковых ставок по облигациям  за  год t при  по формуле для «наведенной» ставки:

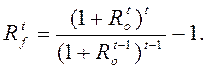
Основную трудность представляет задача экстраполяции величины . Эту величину нельзя экстраполировать по тренду, поскольку в определение ее входит доходность  за счет изменения стоимости  актива, которая меняется нестационарным образом в силу нестационарного характера темпов изменения  чистого денежного потока в прогнозном периоде. Все результаты, полученные до сих пор, опирались только на независимость с.в. .

Предположим теперь дополнительно, что

где  независимые одинаково распределенные с.в. со средними значениями, равными 1. Аналогично предположим, что

где  независимые одинаково распределенные с.в. со средними значениями, равными 1.

Из (21.9) следует, что

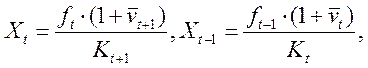
откуда вытекает следующее выражение для доходности  за счет изменения стоимости  актива:

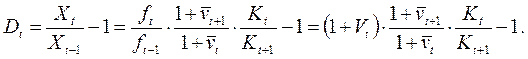         (21.21)

Отсюда имеем:

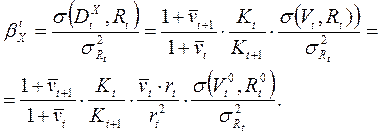                    (21.22)

Из (21) в частности следует, что:

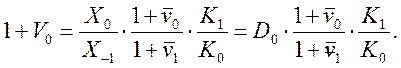               (21.23)

Из (21.11) следует, что:

         

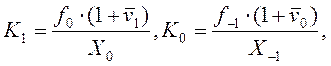
откуда вытекает равенство

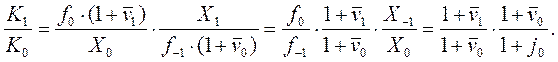          (21.24)

Здесь  –– средний темп изменения стоимости актива за последний год до даты оценки, который обычно известен из экономических обзоров отрасли вместе со средним темпом  изменения чистого денежного потока.

Подставляя (21.24) в (21.23), получим

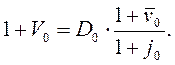                       (21.25)

Подставляя (21.25) в (21.22) с учетом равенства

, справедливого в силу предположения об одинаковом распределении с.в. и , имеем:

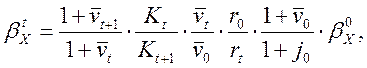               (21.26)

где  бета, определяемая по доходности  актива только за счет изменения стоимости , для последнего периода перед датой оценки, известная из статистических ретроспективных данных.

21.5. Окончательный вид рекуррентного уравнения для K, i_t