Физика \ Физика атомов и молекул

Изменение количества различных частот, наблюдаемых в ИК спектре, страница 4

циклической системы. Только они будут взаимодействовать, поэтому при n = 4k орбиталь j1 во втором порядке теории возмущений повысит энергию на DE = -nb/2, и электрон с орбитали j1 перейдет на две нижние по энергии, занятые 2 электронами (HUMO), орбитали циклической системы, относящиеся к дважды вырожденному неприводимому представлению и имеющие энергию E = a. Так как на этих двух орбиталях окажется три электрона, терм радикала будет 2Еg(u), и эффект Яна-Теллера будет проявляться.

При n = 4k+2 энергия двух вырожденных нижних незаполненных орбиталей E(LUMO) = a - 2bsin(p/n), а энергия j1 орбитали E(j1) = a - nb/2. Так как n = 6, 10, 14…, видно, что n/2 > 2sin(p/n) при этих числах, и орбиталь LUMO окажется ниже по энергии орбитали j1, неспаренный электрон перейдет на вырожденную LUMO, терм будет 2Еg(u), и эффект Яна-Теллера будет проявляться и в этом случае.

2. (500) Для плоской циклической молекулы Hn (n = 4k + 2), относящейся к группе симметрии Dnh, определить количество различных частот колебаний, проявляющихся в КР спектре.

Решение: Для определения количества разных частот строчку характеров колебательной волновой функции необходимо умножить на строчку характеров для тензора поляризуемости, сложить и поделить на порядок группы (для Dnh порядок группы 4n). Произведение характеров для разных операций равно

E – (3n-6)´6;   Cn – (Nc-2)2cosj(1+2cosj)2;     I  – -18NI;   s – 2Ns;   Ns2cosj(-1+2cosj)2.

Для группа Dnh полученная строка будет иметь вид

E

2Cj

2C2j

….2C2kj

C2

(n/2)C2’

(n/2)C2”

6(3n-6)

-4cosj(1+2cosj)2

-4cos2j(1+2cos2j)2

-4cos2kj(1+2cos2kj)2

4

0

4

I

2Sj

2S2j

…2S2kj

sh

(n/2)sv

(n/2)sd

0

0

0

0

2n

4

0

Таким образом, количество различных частот

где j = 2p/n. Расчет слагаемых в сумме приводит к выражениям

Подпись:

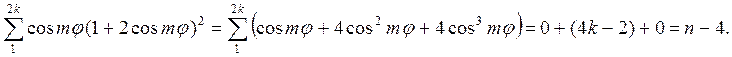
В результате число разных частот равно 4 и не зависит от n.

3. (400) Определить спектр ЭПР p-радикала C7H7, структура которого представлена на рисунке. Все p-центры пронумерованы, чтобы было использовано однотипное обозначение.

Решение: С помощью симметрии можно показать, что неспаренный электрон находится на орбитали

,

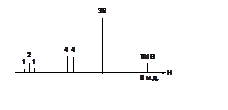
Таким образом, в спектре ЭПР будет проявляться расщепление на 6 эквивалентных a-протонах с константой a = 23/4 Гс. В спектре ЭПР будет 7 линий с соотношением интенсивностей 1:6:15:20:15:6:1.

4. (400) p-радикал C6H7 (5 p-центров) образовался в результате присоединения атома водорода к молекуле C6H6 по одному из 6 p-центров (см. рисунок). Определить изменение спектра ЭПР, если атом H совершает прыжки между двумя эквивалентными центрами (показано на рисунке). Прыжки совершает один и тот же атом водорода. Рассмотреть случаи медленного, среднего и быстрого обмена (определить число линий, относительную интенсивность и константы расщепления).

Подпись: Решение: Линейный альтернантный радикал имеет спиновую плотность r = 1/3 на 3 центрах, с которыми соединены 5 атомов водорода. Таким образом, на 5 эквивалентных a-протонах будет константа расщепления a = 23/3 Гс, и в спектре будет 6 линий с соотношением интенсивностей 1:5:10:10:5:1. На двух b-протонах расщепления нет, так как атом углерода, которому они принадлежат, соединен с немеченными центрами. При медленном обмене каждая линия с вероятностью ½ не обменивается и с той же вероятностью испытывает обмен. По этой причине в случае среднего обмена в спектре ЭПР останется 6 линий с тем же соотношением интенсивностей (общая интенсивность уменьшится в 2 раза). При быстром обмене будет расщепление на 4 эквивалентных a-протонах (не участвующих в обмене) с константой a = 23/3 Гс и на 2 a-протонах с константой в 2 раза меньшей. В итоге в спектре будет 11 линий с соотношением интенсивностей 1:2:5:8:10:12:10:8:5:2:1.

Скачать файл