3. (200) при подогреве замороженной матрицы до температуры 150 К степень поляризации флюоресценции уменьшилась в два раза. Оценить вязкость расплавленной матрицы, если люминесцирующая молекула имеет радиус 5 А.
Решение. Уравнение Левшина – Перрена, описывающее степень поляризации для вращающихся молекул, имеет вид
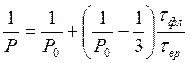, где P0
– степень поляризации для замороженной матрицы без вращения молекул
(определяется геометрией эксперимента), tфл – характерное время высвечивания люминесценции, tвр – характерное время
вращения молекул в расплавленной матрице, которое можно оценить по уравнению
Стокса – Эйнштейна (для сферических молекул)
.
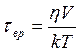В последней формуле h - вязкость расплавленной матрицы, V – объем люминесцирующей молекулы, k – постоянная Больцмана, Т – температура.
Преобразование формулы Левшина – Перрена позволяет получить соотношение
.
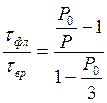Учитывая, что P0 << 3 (максимальная степень поляризации P0 = ½ при возбуждении поляризованным светом), для оценок величины вязкости можно получить выражение
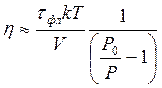
Подставляя в эту формулу tфл » 5 нс = 5´10-9 с, V = (4p/3)R3 = 5.2´10-22 см3, k = 1.38´10-16 эрг/град, T = 150 K и P0/P = 2, получим h » 0.2 пуаз. Отметим, что вязкость воды при комнатной температуре около 0.01 пуаз.
4. (400)
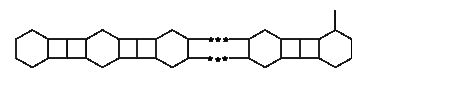
Определить общую протяженность спектра ЭПР (от одной крайней линии до другой)
для p-радикала, строение
которого представлено на рисунке. Количество бензольных колец – N. Выразить ответы через N.
Решение. Достаточно просто определить, что при четном N в спектре ЭПР будут проявляться N+1 a-протонов с константой
.
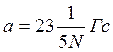В соответствии с этим общая протяженность спектра ЭПР будет
.
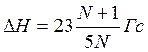При нечетном N в спектре ЭПР будут проявляться N+2 эквивалентных протона с константой СТС
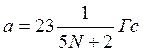
и два протона с константой
.
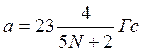В этом случае общая протяженность спектра ЭПР
.
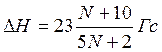5. (400) Определить изменение спектра ЭПР катион-радикала H2+ при включении реакции
H2+
H + H+, когда каждый катион радикал
изолирован в индивидуальной полости цеолита. Представить спектры ЭПР во всех
трех случаях обмена. Считать, что скорости прямой и обратной реакции совпадают.
Решение. В случае отсутствия обмена спектр ЭПР катион-радикала H2+ содержит 3 линии. Если скорости в обоих направлениях равны, концентрации H2+ и атома водорода совпадают. Линии атома накладываются на крайние линии катион-радикала, и исходный спектр при равенстве ширин линий обоих частиц состоит из 3 линий с соотношением интенсивностей 3:2:3. Крайние линии катион-радикала обусловлены случаем, когда оба ядра имеют проекции aa или bb, поэтому они не испытывают обмена. Обмен испытывают центральные линии, которые принадлежат половине от общего количества катион радикалов. Они уширяются при включении обмена, “прыгая” в крайние линии при превращении катион-радикала а атом. В случае среднего обмена эти линии могут исчезнуть из спектра, в котором останутся две линии с расщеплением 510 Гс и с относительной интенсивностью 2:2. В случае быстрого обмена сужение обменивающихся линий приведет к формированию спектра из 4 линий, который можно описать двумя константами: 127.5 и 382.5 Гс. Это соответствует расщеплению на двух неэквивалентных протонах со спиновыми плотностями ¾ и ¼. Первая спиновая плотность отвечает протону который относится к атому водорода (на нем неспаренный электрон находится и в H2+ и в атоме H), а вторая спиновая плотность относится к протону H+ (на нем электрон появляется только в момент существования H2+). Суперпозиция с необменивающимися линиями приведет к 4 линиям с соотношением интенсивностей 2:2:2:2.
Контрольная
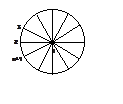
по “Строению Вещества” 29 мая 2003, группы 041, 042, 0431. (500) Будет ли проявляться эффект Яна-Теллера для плоского радикала Hn+1 (см. рисунок), который относится к группе Dnh (использовать теорию возмущений).
Решение: В группе Dnh по полносимметричному представлению преобразуется только орбиталь центрального атома j1 и комбинация
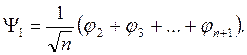
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.