Изменение количества различных частот, наблюдаемых в ИК спектре, страница 2

Задачи на контрольную 29 мая 2002. Группы 941-942-943-843

1. (500) Для плоской циклической молекулы X_N (N = 4k + 2) найти число различных частот колебаний, проявляющихся в ИК спектре. Определить это число при N ® ¥.

Решение. В таблице показаны строчка характеров колебательных функций для циклической плоской молекулы и строка характеров для дипольного момента в группе D_nh. После перемножения этих строк, суммирования и деления на порядок группы (4N) получим число различных частот колебаний, проявляющихся в ИК спектре.

	E	2Cj	2C2j	….	C2	(2k+1)C2’	(2k+1)C2’	I	2Sj	2S2j	….	sh	(2k+1)sV	(2k+1)sd
cQ	3N-6	..-2(1+2cosnj)..			2	0	2	0	0			N	2	0
cd	3	…(1+2cosnj)…			-1	-1	-1	-3	…(-1+2cosnj)…			1	1	1

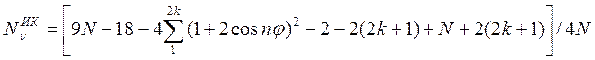
После нахождения суммы и учета того, что j = 2p/N = 2p/(4k+2) = p/(2k+1)

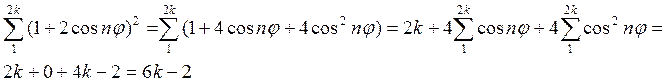
В результате получим

Таким образом, независимо от величины N, в ИК спектре плоской циклической молекулы X_N будет наблюдаться одна частота.

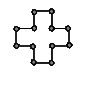
2. (500) Определить, будет ли проявляться эффект Яна-Теллера для молекулы H₁₂, строение которой показано на рисунке (группа D_4h). Ответ обосновать определением вида и энергии МО и основного терма молекулы.

Решение. В таблице представлена строчка характеров преобразования 1s орбиталей всех 12 атомов водорода, являющихся базисом приводимого представления. Его разложение на неприводимые представления показывают симметрию молекулярных орбиталей.

D4h	E	2C4	C2	2C2’	2C2’’	I	2S4	sh	2sv	2sd
c(1s)	12	0	0	2	0	0	0	12	2	0

Г(1s) = 2A_1g + A_2g + 2B_1g + B_2g + 3E_u

Учитывая, что данная молекула является альтернантной системой с симметричным расположением МО, очевидно, что из трех орбиталей типа e_u одна имеет энергию a. Именно на этих двух вырожденных орбиталях будет находится верхняя по энергии пара электронов, которая определяет терм молекулы. По правилам Гунда основным термом будет терм со спином 1, а его орбитальная симметрия будет определяться антисимметричной частью прямого произведения [e_u´e_u]_a.

[e_u´e_u] = A_1g + A_2g + B_1g + B_2g,

[e_u´e_u]_a = A_2g.

Таким образом, основным термом молекулы будет орбитально невырожденный терм ³A_2g, и проявления эффекта Яна-Теллера не будет. Очевидно, что молекула является еще и циклической системой. Это обстоятельство позволяет легко выписать энергию и вид молекулярных орбиталей и определить их симметрию.

E = a + 2b            1A_1g    Y(1A_1g) = (1/)(j₁+j₂+j₃+j₄+j₅+j₆+j₇+j₈+j₉+j₁₀+j₁₁+j₁₂);

E = a + b    1E_u     Y₁(1E_u) = (1/)(j₁+j₂+j₃+j₄+j₅-j₇-j₈-j₉-j₁₀-j₁₁);

E = a + b    1E_u     Y₂(1E_u) = (1/)(j₁+j₂-j₄-j₅-2j₆-j₇-j₈-j₁₀-j₁₁+2j₁₂);

E = a + b              1B_1g    Y(1B_1g) = (1/)(j₁-j₂-j₄+j₅+j₇-j₈-j₁₀+j₁₁);

E = a + b                B_2g    Y(B_2g) = (1/)(j₁+j₂-j₄-j₅+j₇+j₈-j₁₀-j₁₁);

E = a                     2E_u     Y₁(2E_u) = (1/)(j₁-j₃+j₅-j₇+j₉-j₁₁);

E = a                     2E_u     Y₂(2E_u) = (1/)(j₂-j₄+j₆-j₈+j₁₀-j₁₂);

E = a - b               2A_1g    Y(2A_1g) = (1/)(j₁+j₂+j₄+j₅+j₇-j₈+j₁₀+j₁₁);

E = a - b                 A_2g    Y(A_2g) = (1/)(j₁-j₂+j₄-j₅+j₇-j₈+j₁₀-j₁₁);

E = a - b     3E_u     Y₁(3E_u) = (1/)(j₁-j₂+j₃-j₄+j₅-j₇+j₈-j₉+j₁₀-j₁₁);

E = a - b     3E_u    Y₂(3E_u) = (1/)(j₁-j₂+j₄-j₅+2j₆-j₇+j₈+j₁₀-j₁₁-2j₁₂);

E = a - 2b              2B_1g    Y(2B_1g) = (1/)(j₁-j₂+j₃-j₄+j₅-j₆+j₇-j₈+j₉-j₁₀+j₁₁-j₁₂).