8. ДИНАМИЧЕСКАЯ МОДЕЛЬ МАНИПУЛЯТОРА
С УПРУГОЙ СВЯЗЬЮ В СХВАТЕ
Рассмотрим систему схват - деталь промышленного робота при наличии упругой связи между ними (рис.74). Введем следующие системы координат: система О0x0y0zo неподвижна и связана с отверстием; системы Оnxnynzn и Оn+1xn+1yn+1zn+1 подвижные и связаны соответственно с геометрическим центром схвата и центром масс детали. Примем, что в положении равновесия геометрические центры схвата и детали совпадают и деформации упругих элементов равны нулю.
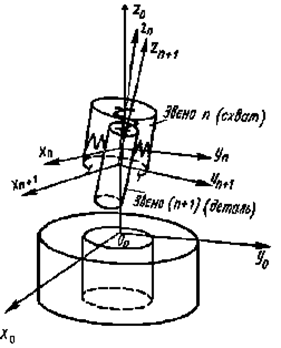 |
Рис. 74. Расчетная схема схвата с упругой связью
Примем, что линейные и угловые жесткости закрепления детали в схвате соответственно равны сx = cy = cz = c; cjx = cjy = cjz = cj, сила упругости Fi = ciDxi, где сi – жесткость i-й упругой связи; Dxi – деформация упругого элемента соответствующей координаты, которая равна смещению xin-й оси относительно xi(n+1) – й, т. е. Dxi = xi(n+1) – xin. Считаем, что угловые отклонения схвата и детали от осей неподвижной системы координат Ооx0y0z0 малы, тогда за обобщенные координаты можно принять углы поворота этих тел относительно осей системы Ооx0y0z0.
Составим уравнения движения схвата манипулятора относительно неподвижной системы координат. Используя уравнения Эйлера для абсолютно твердого тела, закрепленного в одной точке, и теорему об изменении кинетического момента твердого тела, запишем для схвата:
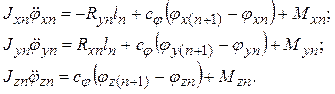
На основе теоремы о движении центра масс запишем:
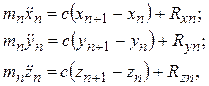
где jxn, jyn, jzn – обобщенные координаты, определяющие угловое положение схвата относительно неподвижной системы координат; jx(n+1), jy(n+1), jz(n+1) – обобщенные координаты, определяющие угловое положение переносимого объекта относительно неподвижной системы координат; Jxn, Jyn, Jzn – моменты инерции схвата относительно осей неподвижной системы координат; Rxn, Ryn, Rzn, Mxn, Myn, Mzn – cилы и моменты в шарнире n, соединяющем схват с предыдущим звеном; mn – масса схвата; Fi – сила упругости i-й связи.
Запишем уравнения движения детали относительно неподвижной системы координат:
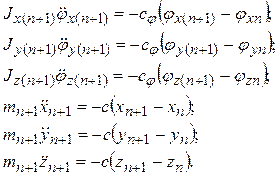
Полученная система дифференциальных уравнений представляет собой динамическую модель упругосвязанной системы манипулятор – деталь.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.