Влияние элементов режима резания и углов резца на главную составляющую силы резания

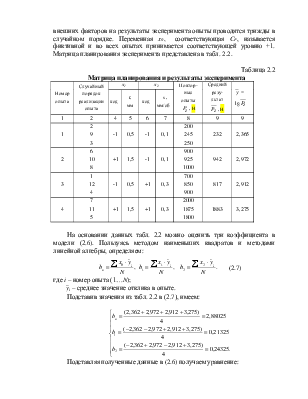
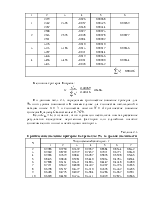
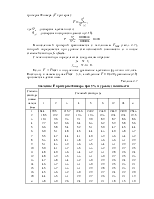
Лабораторная работа № 2

Влияние элементов режима резания и углов резца на главную составляющую силы резания

Цель работы: исследование влияния глубины резания t, подачи s, переднего угла лезвия и главного угла в плане режущего инструмента на составляющие силы резания; аппроксимация результатов измерения составляющих силы резания с применением методов однофакторного и многофакторного анализа (планирование эксперимента).

2.1 Методические основы

Силы резания определяют не только нагрузку на станок, инструмент, деталь, но и температуру резания, период стойкости инструмента, точность обработки и потребляемую мощность.

Зависимость составляющей силы резания от глубины резания и подачи обычно выражают формулой вида

     (2.1)

где Р_Z – тангенциальная (главная) составляющая силы резания;

Р_X – осевая составляющая силы резания;

Р_Y – радиальная составляющая силы резания;

С_P – постоянный коэффициент, зависящий от свойств материала заготовки и условий обработки;

X_P, Y_P – показатели степени влияния глубины резания t и подачи s на составляющую силы резания.

В настоящее время для практических расчетов можно использовать следующие формулы:

2.1.1 Метод однофакторного анализа

Для получения формулы вида (2.1) с использованием метода однофакторного анализа следует иметь в виду, что большинство зависимостей при резании между элементами режима резания и составляющими силы резания описываются степенными функциями, например:

                     (2.2)

Для определения зависимости обрабатывают заготовку с различными подачами, оставляя все другие факторы (скорость, глубину резания и пр.) неизменными. Для каждого принятого при исследовании значения подачи измеряют величины составляющих силы резания.

Обработка результатов динамометрических измерений для нахождения постоянного коэффициента и показателя степени, например в уравнении (2.2), возможна различными способами. Удобнее всего это сделать, приведя степенную функцию к линейному виду. Для этих целей обычно используются функциональные шкалы, которые дают возможность преобразования графиков многих функций к линейному виду. Координатные сетки, построенные с помощью функциональных шкал, называются функциональными. Логарифмическая функциональная сетка используется для спрямления степенных функций.

По данным эксперимента на логарифмическую функциональную сетку наносят точки зависимостей  и  и через них проводят выравнивающие прямые. Уравнения этих прямых, например для зависимости  (см. 2.2):

Поскольку Y_P является угловым коэффициентом прямой, его значение определяется как тангенс угла ее наклона к оси:

где ω – угол наклона прямой (рис. 2.1).

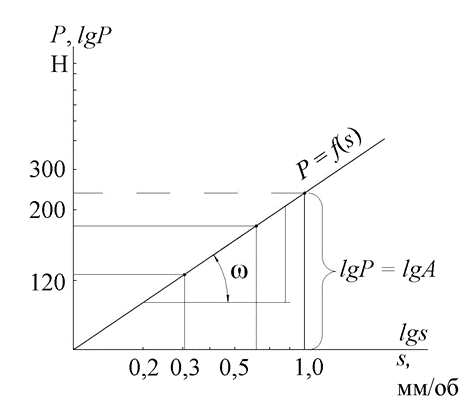
Рис. 2.1. График зависимости силы резания от изменения подачи

Значение коэффициента  А определяется из равенства , которое возможно при , так как в этом случае . Величина А снимается с графика (рис. 2.1).

Так же обрабатываются данные по зависимости между Р и t:

    при t=1

Подсчитав численное значение коэффициентов А и B для частных зависимостей, определяют постоянный коэффициент C_P, зависящий от условий обработки. C_P можно определить совместным решением уравнений:

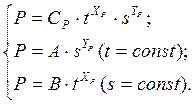
Приравнивая правые части первых двух уравнений, получим:

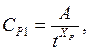
причем, определяя C_P1, вместо глубины резания подставляют величину t = const, при которой получена зависимость , так как эта зависимость действительна только для данной глубины резания.

По аналогии вычислим:

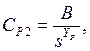
подставляя s = const, при которой подучена зависимость Р = f(t).

По найденным значениям C_P1 и C_P2 определяется среднеарифметическое значение искомого коэффициента:

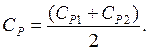
Полученные значения С_P, X_P, Y_P подставляются в уравнение (2.1).

2.1.2 Метод многофакторного анализа

Известно, что физико-механические свойства обрабатываемого и инструментального материалов, геометрические параметры заготовки и инструмента, жесткость в связи с режимом работы станка и особенностями крепления заготовки меняются в определенных пределах. Поэтому многие исследователи считают целесообразным рассматривать процесс резания как плохо организованную систему и изучать ее на основе идей математической статистики.

Метод планирования эксперимента был впервые предложен в 1953 году проф. Дж. Боксом при изучении процессов химической технологии, некоторое время спустя он нашел широкое применение в других областях деятельности человека.

Итак, предлагается модель, описывающая поведение плохо организованной системы. При этом она описывает не систему в целом, а лишь определенный комплекс факторов, интересующий исследователя.

Например, изменение главной составляющей силы резания P_Z в зависимости от глубины резания t и подачи s можно аппроксимировать функцией (2.1).

После логарифмирования уравнение получим полином первой степени:

       (2.3)

Эксперименты планируются на основе многофакторного анализа, т.е. одновременного варьирования всех переменных факторов. Каждая из переменных варьируется на двух или трех уровнях.

При выборе основного уровня и интервалов варьирования собираются и анализируются литературные и производственные данные, а также учитываются предъявляемые требования. В качестве учебного примера, при токарной обработке осевой вагонной стали твердосплавным резцом, выбраны следующие уровни и интервалы варьирования (табл. 2.1). Эти уровни могут быть закодированы при помощи уровней преобразования таким образом, чтобы верхний уровень соответствовал +1, а нижний -1.

За единицу t, s принимается полуразность между значениями верхнего и нижнего уровней факторов.

Таблица 2.1

Уровни факторов и интервалы варьирования