Влияние элементов режима резания и углов резца на главную составляющую силы резания, страница 4

По табл. 2.5 определяем критическое значение t-критерия при числе степеней свободы . В нашем случае для  критическое значение критерия Стьюдента t_крит составляет 2,306. Если , то коэффициент b_i признается значимым, если меньше  – незначимым. В нашем случае все коэффициенты значимы.

Найденное уравнение необходимо проверить на адекватность исследуемому объекту, т. е. установить, насколько хорошо оно прогнозирует данные, получаемые в ходе эксперимента.

Дисперсией адекватности S²_а – это дисперсия, позволяющая оценить, насколько отличается среднее значение отклика функции  для каждого наблюдения в каждом опыте, полученное экспериментальным путем,  и значение ŷ_i в соответствующем наблюдении, полученное путем подставлений значений факторов в найденное уравнение:

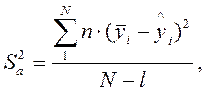
где l - число значимых коэффициентов в уравнении, включая коэффициент при мнимой переменной;

Данные, необходимые для расчета дисперсии адекватности, приведены в табл. 2.6.

Таблица 2.6

Данные для расчета дисперсии адекватности

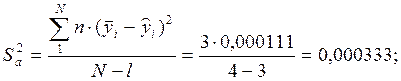
Пригодность уравнения прогнозировать результаты эксперимента в рассматриваемой области с требуемой точностью проверяется путем расчета критерия Фишера (F-критерия):

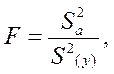
где S²_а– дисперсия адекватности;

S²_(y) – дисперсия воспроизводимости (2.10).

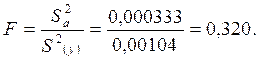
Вычисленный критерий сравнивается с табличным F_табл (табл. 2.7), который определяется при уровне статистической значимости α и числе степеней свободы f_а и f_воспр.

Степени свободы определяются следующим образом:

;

Если  F < F_табл то полученное уравнение адекватно функции отклика. Поскольку в нашем случае F_табл = 5,3, а найденное F= 0,320 уравнение (2.9) признается адекватным.

Таблица 2.7

Значения F-критерия Фишера при 5%-м уровне значимости