Влияние элементов режима резания и углов резца на главную составляющую силы резания, страница 2

Преобразование факторов производится при помощи уравнений:

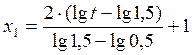;                (2.4)

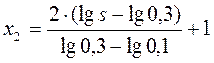.             (2.5)

Здесь за единицу глубины резания принята величина 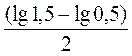, за единицу подачи 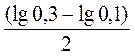. Таким образом, глубина и подача преобразуются путем деления их на принятые единицы.

После введения обозначений в (2.3) имеем:

        (2.6)

где x₁ , x₂ – факторы, преобразованные в безразмерные переменные,

 

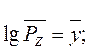
Матрица планирования эксперимента составляется из всех возможных сочетаний значений переменных. Таким образом, количество проводимых опытов N определяется как k^m, где k –количество уровней фактора, а m –количество переменных исследуемых в опытах. В нашем случае N = k^m =2².

Для обеспечения точности получаемых значений и снижения влияния внешних факторов на результаты эксперимента опыты проводятся трижды в случайном порядке. Переменная x₀,  соответствующая C_P, называется фиктивной и во всех опытах принимается соответствующей уровню +1. Матрица планирования эксперимента представлена в табл. 2.2.

Таблица 2.2

Матрица планирования и результаты эксперимента

Номер опыта	Случайный порядок реализации опыта	х1		х2		Повтор- ные опыты ,  Н	Средний резу- льтат , Н	=
		код	t, мм	код	s, мм/об
1	2	4	5	6	7	8	9	9
1	2 9 3	-1	0,5	-1	0,1	200 245 250	232	2,365
2	6 10 8	+1	1,5	-1	0,1	900 925 1000	942	2,972
3	1 12 4	-1	0,5	+1	0,3	700 850 900	817	2,912
4	7 11 5	+1	1,5	+1	0,3	2000 1875 1800	1883	3,275

На основании данных табл. 2.2 можно оценить три коэффициента в модели (2.6). Пользуясь методом наименьших квадратов и методами линейной алгебры, определяем:

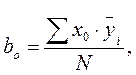
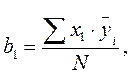
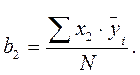         (2.7)

где i– номер опыта (1…N);

 – среднее значение отклика в опыте.

Подставив значения из табл. 2.2 в (2.7), имеем:

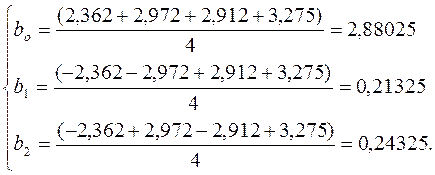
Подставляя полученные данные в (2.6) получаем уравнение:

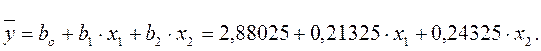    (2.8)

Для получения уравнения (2.8) в натуральных значениях факторов необходимо вместо х₁, х₂, подставить их значения из формул преобразования (2.4), (2.5), а затем провести потенцирование:

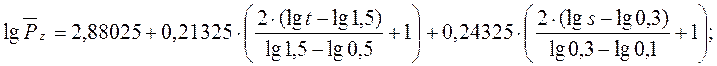
После потенцирования имеем:

             (2.9)

2.1.3 Статистический анализ полученного уравнения

Статистический анализ полученной математической модели состоит из оценки дисперсии воспроизводимости, проверки значимости коэффициентов и проверки адекватности модели.

В случаи проведения в каждом из опытов нескольких наблюдений с одинаковыми значениями факторов, необходимо оценивать однородность  дисперсий всех опытов в эксперименте. Данная характеристика полученной модели называется дисперсия воспроизводимости. Если во всех точках число повторных опытов одинаковое, для ее оценки можно использовать критерий Кохрена.

При этом рассчитывается дисперсия в каждом опыте:

                         

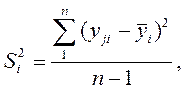
где j– номер наблюдения (1…n);

n – число наблюдений в каждом опыте;

y_ji – значение отклика в наблюдении.

Критерий Кохрена G представляет собой соотношение наибольшей дисперсии, полученной в опытах, к сумме дисперсий всех опытов:

                            

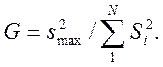
В табл. 2.3 приведены данные для расчета критерия Кохрена. Гипотеза об однородности подтверждается, если расчетное значение этого критерия не превышает табличного.