Таблица 2.3
Данные для расчёта критерия Кохрена
|
Номер опыта |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2,279 2,362 2,267 |
2,305 |
-0,026 +0,057 -0,038 |
0,00068 0,00325 0,00144 |
0,00269 |
|
2 |
2,568 2,623 2,591 |
2,595 |
-0,027 +0,028 -0,004 |
0,00073 0,00078 0,00002 |
0,00077 |
|
3 |
3,176 3,173 3,207 |
3,186 |
-0,010 -0,013 +0,021 |
0,00010 0,00017 0,00044 |
0,00036 |
|
4 |
3,436 3,456 3,473 |
3,455 |
-0,019 +0,001 +0,018 |
0,00036 0,00000 0,00032 |
0,00034 |
|
|
|||||
Величина критерия Кохрена:
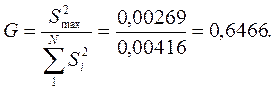
По данным табл. 2.4, определяем критическое значение критерия для 5%-ного уровня значимости. В нашем случае для количества наблюдений в каждом опыте n = 3 и количества опытов N = 4 критическое значение критерия Кохрена Gкр составляет 0,7679.
Если Gкр < G, это значит, что в одном или нескольких опытах рассеяние результатов вследствие неучтенных факторов или случайных ошибок слишком велико и опыты необходимо повторить.
Таблица 2.4
Критические значения критерия Кохрена для 5%-го уровня значимости
|
N |
Число степеней свободы n - 1 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
2 3 4 5 6 7 8 9 10 |
0,9985 0,9669 0,9065 0,8415 0,7808 0,7271 0,6798 0,6385 0,6020 |
0,9750 0,8709 0,7679 0,6838 0,6161 0,5612 0,5157 0,4775 0,4450 |
0,9392 0,7977 0,6841 0,5981 0,6321 0,4800 0,4377 0,4027 0,3733 |
0,9057 0,7457 0,6287 0,5440 0,4803 0,4307 0,3910 0,3584 0,3311 |
0,8584 0,7071 0,5895 0,5063 0,4447 0,3907 0,3595 0,3286 0,3029 |
0,8534 0,6771 0,5598 0,4783 0,4148 0,3726 0,3362 0,3067 0,2823 |
0,8332 0,6530 0,5365 0,4564 0,3980 0,3555 0,3185 0,2901 0,2666 |
Гипотеза об однородности дисперсий принимается, так как экспериментальное значение критерия не превышает табличного. Тогда можно усреднять дисперсии и при подсчете дисперсии воспроизводимости отклика пользоваться формулой:
 (2.10)
(2.10)
Проверку значимости коэффициентов модели производят с помощью t-критерия Стьюдента, представляющего собой отношение абсолютной величины оцениваемого коэффициента к величине его квадратичной ошибки:
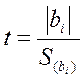 .
.
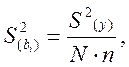 (2.11)
(2.11)
где ![]() – среднее значение дисперсии в опытах (2.10).
– среднее значение дисперсии в опытах (2.10).
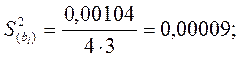
![]()

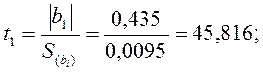

В табл. 2.5 приведены значения t-критерия Стьюдента при 5%-м уровне значимости.
Таблица 2.5
Значения t-критерия Стьюдента при 5%-м уровне значимости
|
Число степе- ней свободы f1 |
Значение t– критерия |
Число степеней свободы f1 |
Значение t– критерия |
|
1 2 3 4 5 6 7 8 9 10 |
12,71 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 |
11 12 13 14 15 16 17 18 19 20 |
2,201 2,179 2,160 2,145 2,131 2,120 2,110 2,101 2,093 2,086 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.