где 
-
объемный расход газа, м3/ч; 
-
плотность природного газа, кг/м3
Для предварительного расчета плотности природного газа компонентами, входящими в его состав в малых долях, можно пренебречь и воспользоваться данными о плотности метана СН4, входящего в состав природного газа, согласно таблице 6.2, в количестве 92,9%.
Температура газа на выходе из турбодетандера при адиабатном расширении 
, ºC [7]:
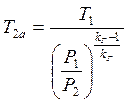, (5.36)
где T2a – температура газа на выходе из детандера при адиабатном расширении, К;
T1 – температура газа на входе в детандер, К;
P1, P2 – давление газа на входе и выходе из детандера, соответственно, МПа;
kГ – показатель адиабаты для метана
,
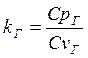(5.37)
где Сp - удельная изобарная теплоемкость метана, кДж/кг·ºС. При температуре 300-1000 К Сp вычисляется по формуле 5.38 выведенной В.А. Заторученко.
СvГ – удельная изохорная теплоемкость метана, кДж/кг·ºС при температуре 300-1000 вычисляется по формуле 5.39, также выведенной В.А. Заторученко.
; (5.38)
. (5.39)
Действительная
температура газа на выходе из детандера 
, ºС
,
(5.40)
где ηТД – к.п.д. турбодетандера.
6.5.3 Математическое моделирование теплообменника - охладителя циркуляционной воды
Цель моделирования теплообменника – выяснить возможность охлаждения в нем
всего объема воды после градирни. Первое, что необходимо вычислить – это
разность температур входящей в теплообменник воды после градирни и выходящей из
него охлажденной газом воды 
.
Согласно закону сохранения энергии, количество теплоты, отданное паром охлаждающей воде при конденсации равно количеству теплоты, полученному водой – уравнение 5.41
, (5.41)
Откуда получаем возможность вычислить разность температур входящей в теплообменник воды после градирни и выходящей из него охлажденной газом воды
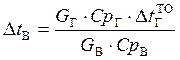, (5.42)
где 
- расход
воды для каждого месяца эксплуатационного года (n=12), кг/ч
- удельная изобарная теплоемкость воды,
кДж/кг·ºС
-величина нагрева газа в теплообменнике, ºС
(5.43)
Примем величину температуры газа на выходе из теплообменника 
, ºС.
Температурой газа на выходе из турбодетандера является температура на входе в теплообменник, ºС
(5.44)
Получив величину охлаждения воды в теплообменнике ,
сделаем вывод о том, является ли такое охлаждение приемлемым в данных условиях.
Далее расчет пойдет согласно пунктам 5.30– 5.34 раздела 5.4.
В виде системы уравнений вышеизложенная математическая модель для исследования возможности охлаждения циркуляционной воды природным газом, расширенным в турбодетандере представлена на рисунке 5.6.
|
Турбодетандер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теплообменник |
|
|
|
|
|
|
|
|
Паровая турбина, конденсатор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 5.6 – Система уравнений математической модели для исследования возможности охлаждения циркуляционной воды природным газом после турбодетандера
5.6 Об адекватности математических моделей
Достоверность научных положений, выводов и рекомендаций обеспечивается:
§ использованием в качестве исходной информации данных с реальной турбоустановки Т-1800210-130 Комсомольской ТЭЦ-3;
§ сравнением результатов расчетов с эксплуатационными данными оборудования и расчетами;
§ корректным использованием математического аппарата;
§ разработкой математических моделей на основе фундаментальных законов и уравнений термодинамики, теплотехники, тепло - и массообмена с учетом рекомендаций нормативных методов расчета.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
(Gвмай
Gвиюнь Gвиюль
Gвавг Gвсент
)
; 
