Базовая математическая модель НПК. Параметры установки. Паровая турбина, страница 4

Таким образом, в уравнении 5.15 имеем два неизвестных  и ts_m.

Чтобы по уравнению 5.15 найти температуру насыщения, найдем по логарифмический температурный напор , ºС

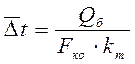,                                               (5.18)

где k_m – расчетный коэффициент теплопередачи, Вт/м²·°С, который по формуле 5.8 зависит от скорости охлаждающей воды в трубках конденсатора в степени 1/2 .

Примечание – Индекс «б» означает, что параметр взят из расчета базовой модели.

Скорость воды в трубках конденсатора изменяется прямопропорционально изменению расхода охлаждающей воды через конденсатор

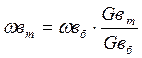                                                  (5.19)

Далее по формуле  5.8 находим коэффициенты теплопередачи для каждого коэффициента кратности циркуляции, которому соответствует своя скорость ωв_m . Возвращаемся к уравнению 5.15 и находим по рассчитанным данным температуру насыщения в конденсаторе, по которой возможно нахождение давления в конденсаторе Рх_m, соответствующего каждому коэффициенту кратности циркуляции.

Энтальпия h₀ остается неизменной в соответствии с базовым вариантом. Энтальпия в конце процесса расширения – функция от давления в конденсаторе и энтропии процесса s₀:

,

По формуле 5.20 находим адиабатный теплоперепад для каждого коэффициента кратности циркуляции:

,                                           (5.20)

Исходя из того, что изменение электрической мощности турбины будет прямопропорционально изменению адиабатного теплоперепада, определяем мощность турбины, МВт

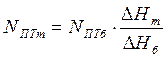           .                (5.21)

Изменение мощности паровой турбины, МВт

                                    (5.22)                                          

Уравнения 5.15 – 5.22 и сопутствующие им уравнения из мат. модели 1 составляют часть второй математической модели, описывающую влияние изменения коэффициента кратности циркуляции на мощность паровой турбины.

5.3.2 Изменение мощности, потребляемой циркуляционным насосом

Мощность, потребляемая циркуляционным насосом возрастает пропорционально изменению сопротивления водяного тракта, которое в свою очередь, зависит от квадрата скорости воды в трубках конденсатора. Таким образом, мощность изменяется прямопропорционально квадрату изменения скорости охлаждающей воды 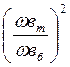. Воспользовавшись уравнениями 5.14 и 5.19, получаем:

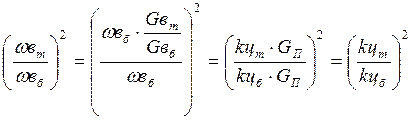                         (5.23)

Мощность, потребляемая циркуляционным насосом , МВт

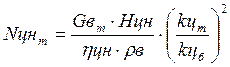                                  (5.24)

Изменение мощности, потребляемой циркуляционным насосом, МВт

                                     (5.25)

Изменение электрической мощности паровой турбины с учетом изменения мощности, потребляемой циркуляционным насосом , МВт:

                                  (5.26)

В виде системы уравнений математическая модель 2 представлена на рисунке 5.2.

Паровая турбина, конденсатор	kцm =(50, 60,70, 80, 90, 100, 110, 120, 130, 140, 150, 160)
Насосная установка
Изменение электрической мощности турбины

Рисунок 5.2 – Система уравнений математической модели для поиска целесообразного коэффициента кратности циркуляции

5.4 Математическая модель 3 – исследование возможности доохлаждения добавочной водой из подземных источников

В рассматриваемую математическую модель входит теплообменник, в межтрубном пространстве которого будет охлаждаться вода после градирни, а по трубкам будет прокачиваться добавочная охлаждающаяся вода из скважины температурой 6 °С в количестве 1800 т/ч.

 

Рисунок 5.3 – Схема теплообменника для охлаждения воды после градирни

Пусть вода, идущая в теплообменник из градирни, будет иметь индекс «В», а добавочная вода из-под земли – «Д». В первом приближении примем что температура охлаждаемой воды понизится в теплообменнике на ∆t_охл^Iградусов меньше температуры поступающей воды из градирни.

Таким образом, получаем температуру охлаждаемой воды на выходе из теплообменника , °С: