Базовая математическая модель НПК. Параметры установки. Паровая турбина, страница 2

Ниже описаны особенности моделирования отдельных элементов НПК ТЭС.

Система уравнений базовой математической модели представлена на рисунке 5.1.

Рисунок 5.1 – Система уравнений базовой математической модели

5.2.1 Паровая турбина

Модель паровой турбины входит в состав математической модели НПК, поскольку условия ее работы зависят от параметров и условий работы конденсационного устройства и системы водоснабжения, а также уровня нагрузки блоков ТЭС. Модель паровой турбины (ПТ) предназначена для определения мощности на клеммах генератора в зависимости от уровня нагрузки блока и давления в конденсаторе.

К моделированию ПТ в составе НПК возможны несколько подхода. При используемом принимается, что изменение давления в конденсаторе влияет только на мощность последней ступени ЧНД турбины и не учитывается изменение внутреннего относительного к.п.д. всех ступеней турбины, кроме последней ступени ЧНД, при изменении расхода пара. Кроме этого принимается, что теплота конденсации пара в конденсаторе постоянна. Поэтому в модели ПТ подробно рассматривается только последняя ступень ЧНД [11].

Для дальнейших расчетов мощности ПТ необходимо по формуле 5.1 найти адиабатный теплоперепад:

,                                             (5.1)

где  - величина адиабатного теплоперепада для каждого месяца (n – январь, февраль, …, декабрь), кДж/кг;  - энтальпия в начале процесса расширения, кДж/кг – функциональная зависимость от начального давления и температуры

;

 - энтальпия в конце процесса расширения, кДж/кг – функция от давления в конденсаторе и энтропии процесса s₀:

,

.

Принимаем, что номинальная электрическая мощность турбины вырабатывалась в том месяце, когда энергия парообразования была максимальной. Т.о. мощность турбины  для каждого месяца , МВт

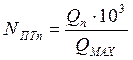,                                            (5.2)

где Q_n, Q_MAX – энергия парообразования каждого месяца и максимальная энергия парообразования в один из месяцев, кДж/кг

,                                              (5.3)

 - удельная теплота парообразования, кДж/кг

.

5.2.2 Конденсационное устройство

Математическая модель конденсатора предназначена для определения давления пара в конденсаторе и гидравлического сопротивления его по воде при различных значениях внешних факторов - расхода и температуры охлаждающей воды, расхода отработавшего в турбине пара, теплоты его конденсации и др. Возможен расчет как поверхностных, так и смешивающих конденсаторов.

Конденсационная установка турбины состоит из поверхностного конденсатора, конденсатных насосов, основных и пусковых эжекторов для удаления воздуха из конденсатора и водяных камер, циркуляционных насосов.

Конденсатор – двухходовой, с общей поверхностью теплообмена 9000 м³, предназначен для работы на пресной охлаждающей воде. По охлаждающей воде конденсатор – однопоточный, разделен на два отсека, позволяющих осуществлять конденсацию пара при разных давлениях, соответствующих температурам последовательно пропускаемой через отсеки воды.

Согласно законa сохранения энергии, количество теплоты, отданное паром охлаждающей воде при конденсации равно количеству теплоты, полученному водой – уравнение 5.4

                                          (5.4)

где    Сp_n - удельная изобарная теплоемкость, кДж/кг·°С:

,

Средняя температура охлаждающей воды t_СРn, ºС

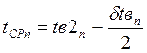                                                       (5.5)

Из уравнения 5.4 найдем расход охлаждающей воды , т/ч

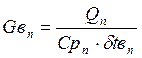                                           (5.6)

Величина коэффициента кратности циркуляции для каждого месяца

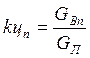.                                             (5.7)