Базовая математическая модель НПК. Параметры установки. Паровая турбина, страница 3

Для дальнейшего расчета модели 2 необходимо рассчитать скорость охлаждающей воды в трубках конденсатора, вывод формулы для расчета скорости можно сделать из формулы, которую В.Л. Семека предложил для расчета коэффициента теплопередачи , Вт/(м²°С) [3]:

 .                                 (5.8)

где    - удельная паровая нагрузка, кг/( м² час),

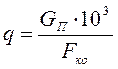;                                              (5.9)

F_ко – площадь поверхности теплообмена, для данной модели конденсатора с учетом загрязнения, м²

F_ко = 6000;

 а – коэффициент, учитывающий влияние загрязнения поверхности, который можно принять равным 0,85;

C_d – поправочный множитель на диаметр трубок конденсатора (при d_н = 16 мм  C_d = 0,947, при d_н = 19 мм  C_d= 1,0, при d_н = 22 мм  C_d= 0,973);

C_t – поправочный множитель на температуру охлаждающей воды при входе в конденсатор (при  = 885, при  = 960, при  = 1000);

Логарифмический температурный напор , ºС

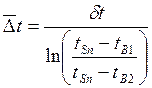.                                                 (5.10)

Таким образом, переходя к расчету скорости охлаждающей воды , м/с, согласно формуле 5.8, получим

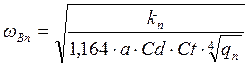,                                       (5.11)

Примем значение коэффициента теплопередачи и температурного напора неизменным для всей поверхности охлаждения конденсатора

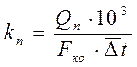.                                          (5.12)

5.2.3 Насосная установка

Подача охлаждающей воды к конденсаторам турбин и нагретой воды к охлаждающим устройствам производится центробежными либо осевыми насосами с электроприводом; на крупных ТЭС широко используются осевые насосы с поворотными лопастями, допускающие плавное регулирование производительности. Математическая модель насосной установки используется для определения мощности, потребляемой циркуляционными насосами в зависимости от расхода охлаждающей воды и требуемого напора насоса.

Мощность циркуляционного насоса в базовом варианте , МВт

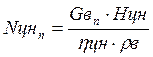,                                               (5.13)

где     Hцн = 100 – напор насоса, кПа;

ηцн = 0,8 – КПД насоса;

ρв = 1000 – плотность жидкости, кг/м³.

5.3 Математическая модель 2 – поиск целесообразного коэффициента кратности циркуляции

Изменение расхода охлаждающей воды возможно при помощи частотно-регулируемого привода насоса, описанного в разделе 4. Для каждого месяца задаемся полем допустимых коэффициентов кратности циркуляции:

kц_m =(50; 60;70; 80; 90; 100; 110; 120; 130; 140; 150; 160).

Далее расчет ведется для каждого месяца по отдельности. Величина расхода пара для каждого месяца остается постоянной, т.е. такой, какая рассчитана в базовом варианте, соответственно, изменяется лишь расход охлаждающей воды, т/ч

                                                (5.14)

5.3.1 Изменение мощности паровой турбины

Для того чтобы определить мощность турбины при новой кратности циркуляции необходимо найти давление в конденсаторе, соответствующее каждому коэффициенту кратности циркуляции и соответствующий этому давлению адиабатный теплоперепад в турбине при начальных давлении P₀ и температуре t₀  до нового давления в конденсаторе Px_m. Индекс «m»соответствует порядковому номеру месяца: m = 1÷12.

Давление в конденсаторе возможно определить по температуре насыщения пара в нем

Px_m=f(ts_m), где ts_m– температура насыщения в конденсаторе, ºС.

Температуру насыщения можно рассчитать по уравнению для логарифмического температурного напора. Для данной математической модели это уравнение принимает форму 5.15.

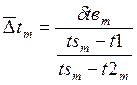                                                 (5.15)

где    - логарифмический температурный напор при m-ном коэффициенте кратности циркуляции, °С;

t1 – начальная температура охлаждающей воды в конденсаторе (примем температуру на входе в конденсатор для каждого месяца),°С;

t2 – конечная температура охлаждающей воды в конденсаторе, °С;       δtв_m– разность температур охлаждающей воды, °С

,                                               (5.16)

С другой стороны, из уравнения 5.4 имеем:

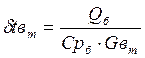 .                                              (5.17)

Воспользовавшись уравнением 5.17 для нахождения δtв_m, по уравнению 5.16  найдем конечную температуру охлаждающей воды в конденсаторе t2_m.