Базовая математическая модель НПК. Параметры установки. Паровая турбина, страница 5

                                              (5.27)

Принимаем температурный напор на выходе из теплообменника , тогда конечная температура добавочной воды ,  °С

Величина нагрева добавочной воды в теплообменнике , °С

,                                           (5.28)

где  - начальная температура добавочной воды, °С (в данном случае );  

Согласно закона сохранения энергии, количество теплоты, отданное паром охлаждающей воде при конденсации равно количеству теплоты, полученному водой – уравнение 5.4. Располагая величиной расхода охлаждаемой воды G_В, подсчитанной в базовом варианте и расходом добавочной воды G_ДВ, получим величину охлаждения воды, поступающей из градирни в теплообменник

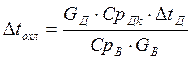  .                                    (5.29)

Путем итерационных вычислений добиваемся сходимости величин  и  с погрешностью < 1%. Далее математическая модель несет в себе элементы базовой и второй математической модели по поиску целесообразного коэффициента кратности циркуляции, но уже с меньшей температурой охлаждающей воды . Т.к. проблема недоохлаждения воды в конденсаторе стоит перед станцией только в теплое время года, рассмотрим влияние добавочного охлаждения для пяти теплых месяцев года: мая, июня, июля, августа, сентября.

Математическая модель разделится на две части: в первой проверим эффективность охлаждения добавочной водой на базовых параметрах, т. е. при базовом коэффициенте кратности циркуляции; во второй - суммарный эффект от первого мероприятия и второго (добавочное охлаждение и оптимальная кратность циркуляции).

В виде системы уравнений первая часть математической модели по исследованию возможности доохлаждения добавочной водой из подземных источников представлена на рисунке 5.4. В обозначениях величин индекс k соответствует номеру месяца. k=5: 1 - май, 2 - июнь, 3 - июль, 4 -август, 5 -сентябрь.

Рисунок 5.4 – Система уравнений математической модели для исследования возможности доохлаждения воды после градирни водой из скважины

Вторая часть математической модели по исследованию возможности доохлаждения добавочной водой из подземных источников представляет собой расчет совместного эффекта от добавочного охлаждения при целесообразной кратности циркуляции, т.е. расход охлаждающей воды, поступающей на конденсатор будет изменен по сравнению с базовым вариантом – величина расхода охлаждающей воды будет взята из математической модели 2.

В соответствии с вышеизложенным, мощность, потребляемая цирк насосом , МВт

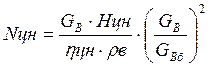,                                     (5.30)

где - базовый расход воды в исследуемых месяцах, т/ч

Остальные параметры, кроме ,  также взяты из базовой модели.

Для того, чтобы определить мощность турбины при новой температуре поступающей в конденсатор охлаждающей воды и оптимальной кратности циркуляции необходимо найти давление в конденсаторе, соответствующее каждому коэффициенту кратности циркуляции и соответствующий этому давлению адиабатный теплоперепад в турбине при начальных давлении P₀ и температуре t₀  до нового давления в конденсаторе Px.

Давление в конденсаторе возможно определить по температуре насыщения пара в нем

Px=f(ts),

Температуру насыщения ts можно рассчитать по уравнению для логарифмического температурного напора, для данной математической модели это уравнение принимает форму аналогичную уравнению 5.15. Для чего по уравнению 5.31 определим перепад температур охлаждающей воды, °С

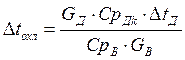 .                                              (5.31)

По уравнению 5.16 найдем конечную температуру охлаждающей воды в конденсаторе t₂.

Скорость воды в трубках конденсатора, согласно формуле 6.2.9 изменяется прямопропорционально изменению расхода охлаждающей воды через конденсатор