Математическая постановка задач целочисленного линейного программирования может быть записана в виде: необходимо найти
такой целочисленный вектор Х=(х1, х2, …, хn), что функция линейного вида z(x)=c1x1+ c2x2+ c3x3+ … + cnxn→max (или min), и удовлетворяет системе линейных неравенств:
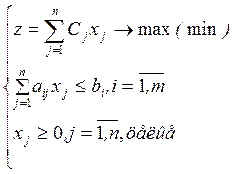 (4.1)
(4.1)
Таким образом, главное отличие задач ЦЛП от задач ЛП (1.2) в том, что ОДР задачи ЦЛП является дискретным множеством. В связи с чем, можно выделить следующие особенности множества допустимых решений D задач ЦЛП: множество является несвязным и невыпуклым.
Решение задач ЦЛП графическим методом во многом схоже с решением графическим методом задач ЛП, рассмотренное во второй главе. Отличие в том, что в связи с дискретностью ОДР решение может располагаться только в точках с целочисленными координатами, и мысленный параллельный перенос прямой ЦФ в направлении оптимума производится до самой дальней целочисленной точки.
Этапы решения графическим методом.
1. Построение ОДР.
2.
Построение радиус-вектора ![]() (градиента целевой
функции) и линии уровня ЦФ.
(градиента целевой
функции) и линии уровня ЦФ.
3.
Мысленный параллельный перенос прямой ЦФ по направлению (в случае если задача
решается на max) или против направления (в случае если задача
решается на min) вектора ![]() до самой дальней
целочисленной точки, принадлежащей ОДР. Найденная таким образом точка и будет
являться решением задачи.
до самой дальней
целочисленной точки, принадлежащей ОДР. Найденная таким образом точка и будет
являться решением задачи.
Рассмотрим следующий пример. Пусть дана задача максимизации линейной целевой функции при заданных ограничениях:
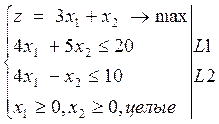
Согласно приведенной выше последовательности решения графическим методом в первую очередь строится ОДР задачи, которая представляет собой множество точек, лежащее в узлах целочисленной решетки, ограниченной прямыми, заданными соответствующими ограничениями-неравенствами L1 и L2 и ограничениями на неотрицательность переменных x1 и x2 (см. рис. 4.1).
На рис. 4.1 показан
радиус-вектор ![]() из точки начала координат
в точку (3,1). Координаты точки определяются по формуле (2.1) - это
коэффициенты целевой функции. Линия уровня ЦФ строится перпендикулярно
радиус-вектору
из точки начала координат
в точку (3,1). Координаты точки определяются по формуле (2.1) - это
коэффициенты целевой функции. Линия уровня ЦФ строится перпендикулярно
радиус-вектору ![]() . На рис. 4.1 она проведена
через начало координат.
. На рис. 4.1 она проведена
через начало координат.
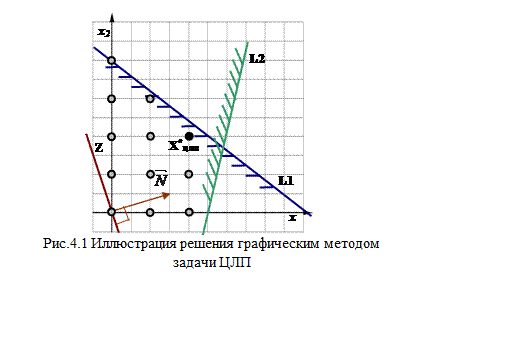
Мысленный параллельный
перенос прямой ЦФ z по направлению радиус-вектора ![]() (т.к.
задача решается на max) до самой дальней целочисленной точки ОДР
дает точку X*цлп. Найденная точка с координатами (2,2) является решением
задачи.
(т.к.
задача решается на max) до самой дальней целочисленной точки ОДР
дает точку X*цлп. Найденная точка с координатами (2,2) является решением
задачи.
Ответ: 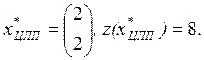 .
.
Одним из универсальных методов решения задач ЦЛП является метод ветвей и границ, он представляет собой эффективную процедуру перебора целочисленных допустимых решений.
Если задача ЦЛП приведена к виду (4.1) , то порядок решения методом ветвей и границ следующий:
1. Задача ЦЛП решается как
задача ЛП, т.е. ограничения целочисленности переменных не учитываются.
Полученное решение ![]() и значение ЦФ
и значение ЦФ ![]() заносится в вершину 1 дерева решений
(см. рис.4.2). Полученное
заносится в вершину 1 дерева решений
(см. рис.4.2). Полученное ![]() – это верхняя
граница оптимального решения задачи ЦЛП.
– это верхняя
граница оптимального решения задачи ЦЛП.
2. Производится выбор переменной, имеющей не целое значение, по которой будет производится ветвление. В случае, если решение имеет несколько дробных переменных, необходимо применять правило выбора переменной. Одно из обычно применяемых правил – это выбор переменной, имеющей наибольшую дробную часть. Другой способ выбора – по переменной имеющей максимальное значение коэффициента сj в ЦФ. Можно применять любое из правил, однако в ходе решения рекомендуется придерживаться одного из них.
3. Пусть xS – выбранная переменная с дробным значением, тогда текущая вершина ветвится на две новые вершины, каждая из которых соответствует двум задачам:
- первая задача (ЛП1) образуется путем
добавления в предыдущую модель нового ограничения вида![]() ;
;
- вторая задача (ЛП2) - ограничения![]() .
.
Здесь ![]() -
это целая часть числа a, т.е. наибольшее целое, не превышающее a. Например,
[27,6]=27 , [0,8]=0.
-
это целая часть числа a, т.е. наибольшее целое, не превышающее a. Например,
[27,6]=27 , [0,8]=0.
4. Решаются две полученные задачи ЛП1 и ЛП2. Если получено допустимое (целочисленное) решение, то обновляем значение нижней границы Zн – максимальное значение из всех полученных на данный момент допустимых решений.
5. Выбираем вершину для ветвления. Для этого проверяем вершины в дереве на прозондированность. Будем считать вершину прозондированной, если в соответствующей вершине задаче ЛП:
- получено целочисленное решение;
- задача ЛП не имеет решений;
- значение ЦФ не превосходит текущей нижней границы Zн.
Определив непрозондированные вершины, выбираем любую из них для ветвления. Обычно, если их несколько, то выбирают вершину с максимальным значением Z.
6. Повторяем шаги 2-5 до тех пор, пока все вершины в дереве не будут
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.