Таблица, устанавливающая соответствие между значениями случайной величины и их относительными частотами, называется статистическим распреДелением случайной величины Х
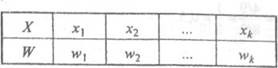
Например, для выборки (3, 2, —1, 2, 3,0) вариационный ряд имеет вид
![]() О, 2, 3), п = б,
О, 2, 3), п = б,  = 1, п, = 1, = 2, = 2, а
статистическое распределение —
= 1, п, = 1, = 2, = 2, а
статистическое распределение —
Для непрерывной случайной величины Х ее статистическое распределение целесообразно представить в виде интервальной таблицы

где Wi — относительная частота попадания случайной величины в интервал (4-1, 4). При этом если случайная величина принимает значений, равных „З, то для четного половину этих значений относят к интервалу 4), а вторую половину — к интервалу (4, 4+1). Для нечетного к левому интервалу
относят значений, а к правому интервалу значений. 2 2
![]() Функция определяющая для каждого
значения х относительную частоту Щ события Х х (где пх — число наблюдений, при
которых наблюдалось значение, меньшее х): называется эмпирической функцией
распределения. При этом функция F(x) распределения генеральной совокупности
называется теоретической функцией распреДеления.
Функция определяющая для каждого
значения х относительную частоту Щ события Х х (где пх — число наблюдений, при
которых наблюдалось значение, меньшее х): называется эмпирической функцией
распределения. При этом функция F(x) распределения генеральной совокупности
называется теоретической функцией распреДеления.
Эмпирическая функция распределения Fn(x) соответствует статистическому распределению и при возрастании п стремится по вероятности к функции ах), т.е. для любого х R и любого Е > О имеет место равенство
lim POFn(x)— ![]() = О.
= О.
Это означает, что при больших п эмпирическая функция распределения ![]() хорошо приближена к теоретической
функции распределения ах).
хорошо приближена к теоретической
функции распределения ах).
22
Для наглядного изображения статистических распределений строят различные графики.
Если Х — дискретная случайная велйчина, строится ломаная, отрезки которой соединяют точки (х, , щ), (Ч, ик), (хк, Ч). Такая ломаная называется полигоном распределения.
Для иллюстрации распределения непрерывной
случайной величины Х строятся диаграммы, называемые гистограммами. Для лого
интервал, в котором заключены все наблюдаемые значения, разбивается на равные
части с шагом ![]() 1, 2 , К, и для каждого i
определяется сумма частот
1, 2 , К, и для каждого i
определяется сумма частот
вариант, попавших в интервал (4-1, 4).
 Гистограмма
частот представляет собой ступенчатую фигуру, состоящую из прямоугольников,
основаниями которых являются отрезки Ц, з, а высоты равны
Гистограмма
частот представляет собой ступенчатую фигуру, состоящую из прямоугольников,
основаниями которых являются отрезки Ц, з, а высоты равны ![]() , К.
Площадь гистограммы частот равна
, К.
Площадь гистограммы частот равна
сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются отрезки
![]() , а высоты равны
, а высоты равны ![]() К. Площадь гистограммы
К. Площадь гистограммы
относительных частот равна сумме всех относительных частот, т.е. единице. Гистограмма относительных частот позволяет приближенно судить о функции плотности распределения, поскольку при достаточно больших п и малых h ломаная, соединяющая середины верхних горизонталей прямоугольников. приближена к функции плотности. Указанную ломаную будем называть ломаной гистограммы.
Выборочным среДним значением случайной величины Х, заданной статистическим распределением, называется выражение
или
 аналогично определяется генерааьное
среДнее значение
аналогично определяется генерааьное
среДнее значение
![]() (1)
(1)
где [У . Так как -Т =Й — вероятность, с которой величина Х принимает
значение то равенство (1) переписывается в виде
23
|
хг = + Х2А+... +Х,И. |
![]()
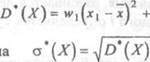
![]()
![]() В соответствии с
законом больших чисел при достаточно большом п выборочное среднее значение хв
приближенно равно математическому ожиданию М(Х). Поэтому для больших п часто
считают, что хв = М(Х).
В соответствии с
законом больших чисел при достаточно большом п выборочное среднее значение хв
приближенно равно математическому ожиданию М(Х). Поэтому для больших п часто
считают, что хв = М(Х).
Статистической Дисперсией случайной величины Х, заданной статистическим распределением, называется выражение
+
w2(x2 2![]()
Величина (Х) называется среДним кваДратичным
отклонением.
При большом объеме выборки имеет место следующее приближенное
равенство: Ы (Х) Ц Х). Поэтому для достаточно больших п часто считается, что D•
(Х) = Ц Х) и о • (Х) =![]()
Для подсчета величины В (Х) пользуются формулой
ПРИМЕР 4
В результате испытаний случайная величина
Х приняла следующие значения: хо- 2, 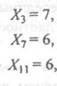 Хв= 1,
Хв= 1,
Требуется:
![]() ) построить статистическое
распределение;
) построить статистическое
распределение;
2) построить эмпирическую функцию распределения;
З) изобразить полигон распределения;
4) считая величину Х непрерывной, составить таблицу статистического распределения, разбив промежуток (О; 10) на пять участков, имеющих одинаковые длины; построить гистограмму относительных частот и ее
ломаную;
5) найти выборочное среднее значение, статистическую дисперсию и среднее квадратичное отклонение случайной величины Х.
Решение
1. Составим таблицу частот:
|
х |
2 |
З |
5 |
6 |
7 |
9 |
|
|
2 |
2 |
З |
2 |
||||
|
Так как объем выборки вид |
равен 12, то статистическое распределение имеет |
||||||
|
2 |
з |
5 |
6 |
7 |
9 |
||
|
2/12 |
2/12 |
1/12 |
3/12 |
2/12 |
1/12 |
||
|
т.е. |
|||||||
|
х |
2 |
З |
5 |
6 |
7 |
9. |
|
|
w |
0,167 |
0,167 |
0,083 |
0,25 |
0,167 |
0,083 |
0,083 |
Контроль: 0,167 + 0,167 + 0,083 + 0,25 + 0,167 + 0,083 + 0,083 = (при округлении нужно учитывать, что сумма относительных частот должна быть равна единице).
2. Имеем

График функции Е изображен на рис. 9.
3. Возьмем на плоскости точки О; 0,167), (2; 0,167), (3; 0,083) и т.д. Последовательно соединив эти точки отрезками, получим полигон распределения (см. рис. 10).
|
0.75 0.5 0,25 |
|
|
|
2 4 5 6 7 8 9 Рис. 9 |
|
24 |
25
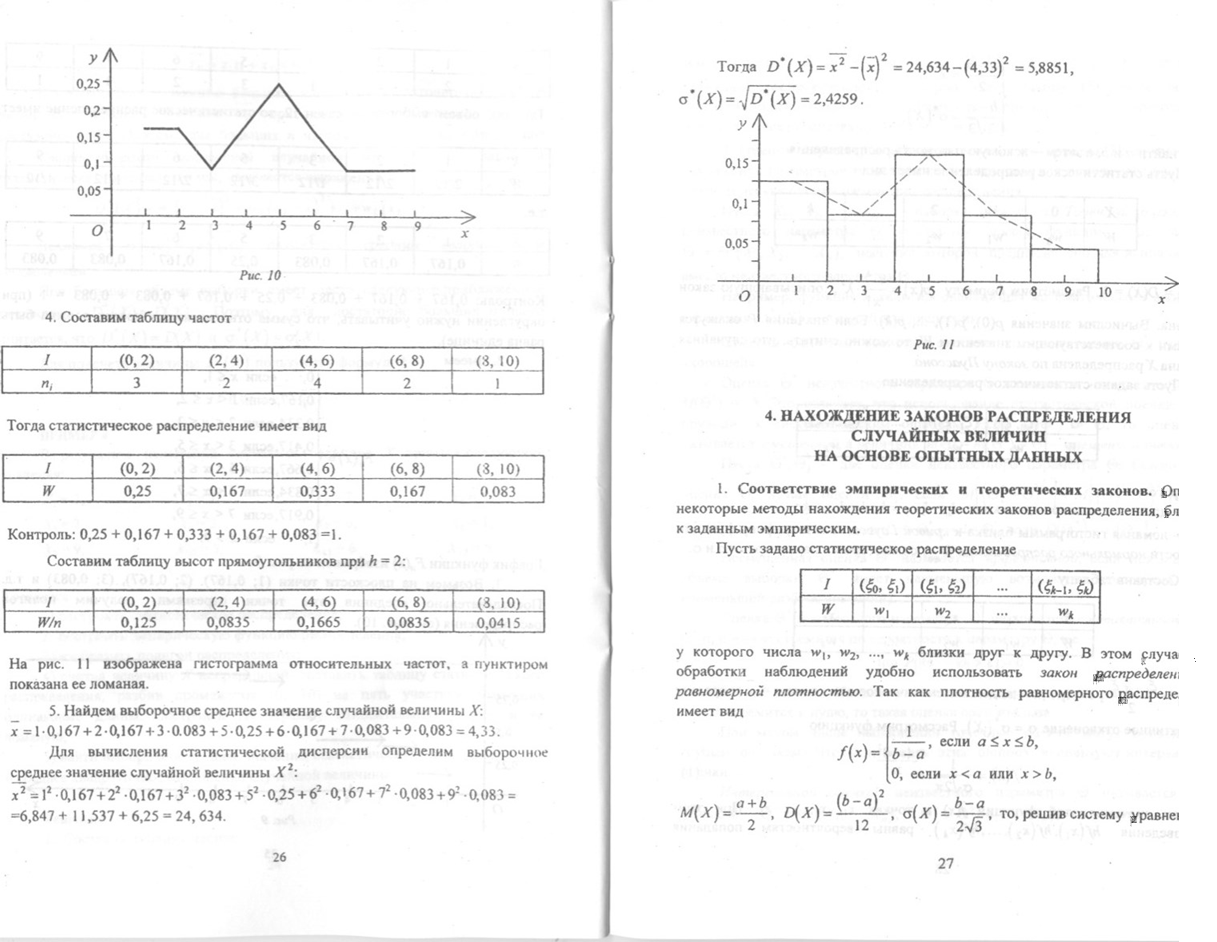 Рис. 10
Рис. 10![]()
4. Составим таблицу частот
На рис. изображена гистограмма относительных частот, а пунктиром показана ее ломаная.
5. Найдем выборочное среднее значение случайной величины Х:
= 4,33.
Для вычисления статистической дисперсии определим выборочное среднее
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.