Вязкость жидкостей и лобовое сопротивление, испытываемое телами, движущимися в жидкости

ЛАБОРАТОРНАЯ РАБОТА № 2 - 2

ЦЕЛЬ РАБОТЫ: ознакомиться с методом измерения коэффициента динамической вязкости жидкости.

ОБОРУДОВАНИЕ: цилиндрический сосуд с жидкостью и двумя кольцевыми метками, шарик, микрометр, секундомер, линейка, термометр.

1. ВЯЗКОСТЬ ЖИДКОСТЕЙ И ЛОБОВОЕ СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛАМИ, ДВИЖУЩИМИСЯ В ЖИДКОСТИ.

Между слоями движущейся жидкости возникает внутреннее трение (вязкость), связанное с торможением более быстро движущихся слоев теми слоями, которые движутся более медленно.

Если жидкость движется по трубе, полностью заполняя её, то слой, прилипший к стенкам трубы, значительно тормозит слой, движущийся вдоль стенок, а последний тормозит следующий внутренний слой, так что скорость течения в трубе изменяется в сечении трубы от нулевого значения у стенок трубы до наибольшего на оси трубы (рис.1). Как показывает опыт, сила внутреннего трения между соприкасающимися слоями направлена по касательной к поверхности слоев, пропорциональна общей площади S слоев и зависит от того. Насколько быстро меняется скорость течения жидкости при переходе от слоя к слою (рис.1) - по оси Z, а именно, пропорциональна градиенту скорости:

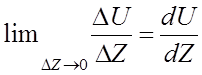
Если обозначить коэффициент пропорциональности через h (это так называемый коэффициент динамической вязкости), то сила внутреннего трения (вязкости) между соприкасающимися слоями:

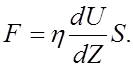
Какова причина внутреннего трения в жидкостях (а так же в газах)?

В протекающей жидкости на скорость беспорядочного движения молекул V наложена переносная скорость U течения жидкости, различная для разных слоев. Молекулы, хаотично перемещаясь из медленно текущих слоев в более быстрые, приносят с собой меньший импульс mU упорядоченного движения, чем имеют уходящие отсюда молекулы, и замедляют движение слоя. Это замедление рассматривается как результат действия силы трения (вязкости).

Тело, обтекаемое жидкостью или движущееся в жидкости, испытывает силу сопротивления, называемую силой лобового сопротивления. При малых скоростях течения жидкости (или движения тела в жидкости) лобовое сопротивление - результат внутреннего между слоем, прилипшим к телу, и соседними слоями. В этом случае сила лобового сопротивления, как показывает опыт, пропорциональна произведению коэффициента вязкости среды на линейные размеры поперечного сечения и движения тела (закон Стокса):

Для частного случая тел шарообразной формы сила лобового сопротивления выражается формулой:

где коэффициент a, найденный экспериментально, равен 6p т.е. в этом случае:

2. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ДИНАМИЧЕСКОЙ ВЯЗКОСТИ ЖИДКОСТИ ПО МЕТОДУ ПАДАЮЩЕГО ШАРИКА.

Если шарик опустить в воду, он начнёт двигаться вниз и на него будут действовать три силы: сила тяжести Р, направленная вниз, выталкивающая сила F₁, направленная вверх, и сила лобового сопротивления F направленная также вверх (рис.2). По динамическому закону Ньютона равнодействующая всех внешних сил равна произведению массы шарика на ускорение его движения:

P – F₁ – F = ma

где: m - масса шарика, а, -  ускорение его падения в жидкости.

Вес шарика:

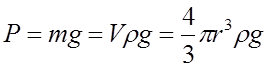, где V и r - объём и радиус шарика; r - плотность вещества шарика.

Выталкивающая сила по закону Архимеда равна весу жидкости, взятой в объёме тела, т.е.:

,

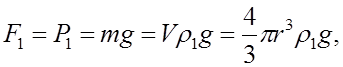где r₁ - плотность жидкости.

Сила лобового сопротивления F выражается формулой (З):

F = 6phUr,

где U - скорость падения шарика.

Вначале движение шарика будет ускоренным, так как сила P не уравновешивается силами F₁ и F вследствие малости силы лобового сопротивления F. Но по мере возрастания скорости U будет возрастать сила лобового сопротивления F, пропорциональная этой скорости U. Наконец, при некотором значении U сила лобового сопротивления вместе с выталкивающей силой F₁ уравновесит силу тяжести, и движение шарика станет равномерным. Из равенства сил:

P = F₁ + F                      ()

или:

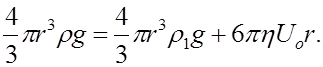
Находим коэффициент вязкости жидкости:

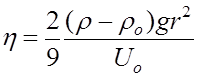
Формула (9) получена в предложении, что устанавливающая скорость U_o движения шарика достаточно мала, иначе будут образовываться вихри, и сила лобового сопротивления будет выражаться иначе. Скорость падения шарика будет достаточно малой, если взять шарик с небольшой массой, чтобы сила лобового сопротивления уравновесила вес шарика в жидкости уже при небольшой скорости движения U_o. Скорость равномерного движения шарика U_o определяется по промежутку времени t в течение которого шарик проходит в жидкости расстояние l между кольцевыми метками (рис.2):

U_o = l/t

Таким образом, расчетная формула будет иметь вид:

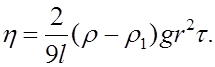
Верхняя метка должна находиться на таком расстоянии ниже поверхности жидкости, чтобы движение шарика при прохождении метки было уже равномерным. Нижняя метка должна находиться выше дна сосуда настолько, чтобы на движение шарика дно не оказывало влияния.