Если в среде некоторого направления устанавливаются гармонические колебания с одинаковой частотой и фазой, нос различной амплитудой, то такое явление называется стоячей волной. Если амплитуда стоячей волны в заданном направлении распределена по гармоническому закону, то стоячая волна называется гармонической. Гармоническая плоская стоячая волна получается в результате интерференции (сложения) двух бегущих в противоположные стороны плоских гармонических волн с одинаковыми амплитудой и частотой и с постоянной разностью фаз, например в результате интерференции бегущей и отраженной плоских волн.
Уравнение бегущей в направлении r плоской волны имеет вид (2), уравнение отраженной в том же направлении волны в той же точке будет отличаться знаком перед r и может отличаться по фазе на некоторую постоянную величину jo:
lo’ = locos[w(t + r/V) + jo].
В результате интерференции обеих волн колебание в рассматриваемой точке будет происходить по закону
lp = l + l’ = locos[w(t – r/V)] = locos[w(t + r/V) + jo] = 2locos(wr/V + jo/2)cos(wt + jo/2)
или
lp = Acos(wt + jo/2) (10)
где
А = 2locos(wr/V + jo/2) (11)
Т.е. в каждой точке будет происходить гармоническое колебание с частотой интерферирующих воли и с амплитудой А, изменяющейся в заданном направлени по гармоническому закону. Это и означает возникновение гармонической плоской стоячей волны. Стоячая волна несмотря на свое название, не связана с распространением энергии в пространстве и представляет собой установившееся колебание особого режима.
Точки, в которых амплитуда A(r) = 0, называются узлами: в этих точках смещение lp = 0 в любой момент времени t. Точки, в которых амплитуда имеет максимальную абсолютную величину, называются пучностъю стоячей волны.
Узлы получаются при cos(wr’K/V + jo/2) = 0.
Т.е., если wr’K/V + jo/2 = (2К + 1)p/2 (K = 0,1,2, …..)
rK’ = V/w[(2K + 1)p/2 - jo/2].
Так как w = 2p/T, а l = VT, выражение распределения узлов стоячей волны (12) в направлении r примет вид:
rK’ = (2K + 1)l /4 - ljo/4p. (13)
Пучности получаются при
|cos(wrK”/V + jo/2)| = 1
wrK”/V + jo/2 = Kp, rK” = Kl/2 - ljo/4p (14)
В пучностях амплитуда А = 2lo, т.е. вдвое больше амплитуды каждой из бегущих волн.
Расстояние между узлом и соседней пучностью равно четверти длины волны:
rK’ - rK” = [(2K + 1)l/4 - ljo/4p] – (Kl/2 - ljo/4p) = l/4. (15)
Расстояние между соседними узлами или между соседними пучностями равно половине длины волны. Полученные результаты можно представить наглядно в виде последовательности моментальных положений гармонической стоячей волны (рис.1) и сравнить с последовательностью моментальных положений бегущей гармонической волны (рис.2).
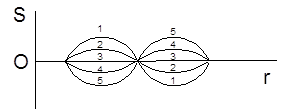
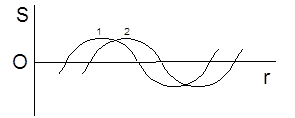
Рис.1 Рис.2
Зная частоту n звуковой волны, создаваемой генератором, и измеряя расстояние между пучностями образовавшейся в трубке стоячей звуковой волны, т.е. находя длину l звуковой волны, по формуле (8) можно найти скорость V звука в воздухе.
Зная скорость V звука в воздухе, можно найти показатель адиабаты g. Для воздуха (отношение теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме). Скорость звука в газах
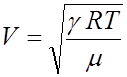 (16)
(16)
где R - универсальная газовая постоянная, m - масса киломоля газа, Т - абсолютная температура. Из равенства (16) находим
g = mV2/RT.
Чтобы вычислить показатель адиабаты g для воздуха, нужно знать температуру Т воздуха и скорость звука V в воздухе при этой температуре.
Для измерения скорости звука служит специальная установка ( рис 3). Звуковые колебания в трубке с воздухом возбуждаются телефоном T, мембрана которого приводится в движение переменным током звуковой частоты от генератора Г3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.