Математика \ Математические основы проектирования ЭС

Проверка гипотезы о нормальном законе распределения статистических данных методом моментов и методом вероятностных сеток

Страницы работы

Содержание работы

Цель работы: Проверка гипотезы о нормальном законе распределения статистических данных методом моментов и методом вероятностных сеток.

В качестве однотипных радиоэлементов использовались резисторы с номинальным сопротивлением 1 Ком.

Измеренные значения сопротивлений, отсортированные в возрастающем порядке (Ом):

960	971	975	978	981	984	986	990	992	997
961	971	975	979	981	984	986	990	993	997
961	972	975	979	981	984	987	990	993	998
964	972	976	979	982	985	987	990	994	999
965	972	976	979	982	985	987	990	994	999
967	973	976	980	982	985	987	990	995	999
968	973	976	980	983	985	988	991	995	1000
968	974	977	980	983	985	988	991	995	1000
969	974	977	980	983	986	989	991	995	1001
970	974	977	981	983	986	989	991	996	1010

Разделим все значения на 10 интервалов: R_min = 960, R_max = 1010; .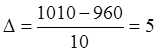

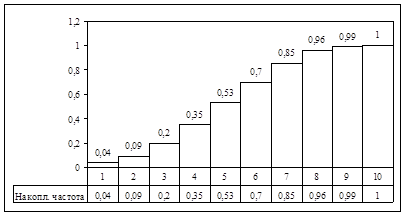
Интервал	Середина интервала	Частота m_i	Относит. частота	Накопл. частота	Относит. накопл. частота
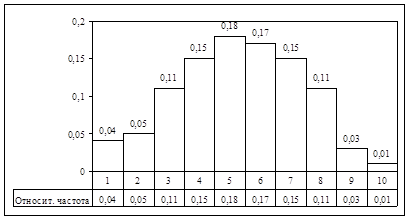
960-965	962,5	4	0,04	4	0,04
965-970	967,5	5	0,05	9	0,09
970-975	972,5	11	0,11	20	0,2
975-980	977,5	15	0,15	35	0,35
980-985	982,5	18	0,18	53	0,53
985-990	987,5	17	0,17	70	0,7
990-995	992,5	15	0,15	85	0,85
995-1000	997,5	11	0,11	96	0,96
1000-1005	1002,5	3	0,03	99	0,99
1005-1010	1007,5	1	0,01	100	1

Среднее арифметическое значение параметра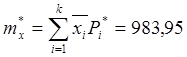

Статистическая дисперсия , .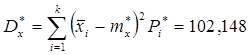

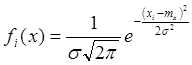
Теоретическое распределение:

Теоретическая вероятность попадания параметра x в i – ый интервал: .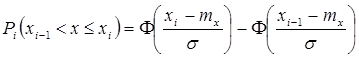

Интервал	Относительная частота,	Вероятность,
960-965	0,04	0,021	0,016000
965-970	0,05	0,053	0,000211
970-975	0,11	0,104	0,000325
975-980	0,15	0,160	0,000628
980-985	0,18	0,193	0,000930
985-990	0,17	0,184	0,001052
990-995	0,15	0,138	0,001119
995-1000	0,11	0,081	0.010000
1000-1005	0,03	0,038	0,001501
1005-1010	0,01	0,014	0,000981

Медиана – 983 Ом

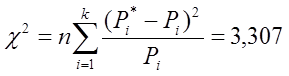
Мода – 990 Ом

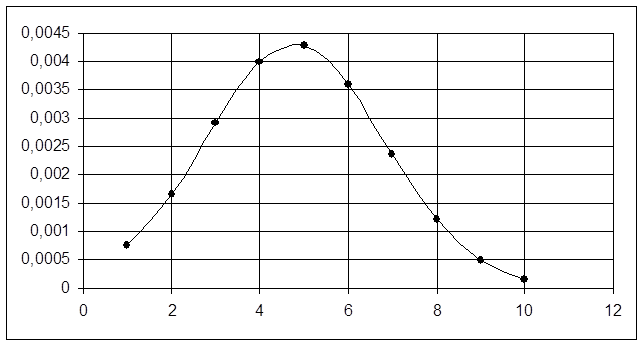
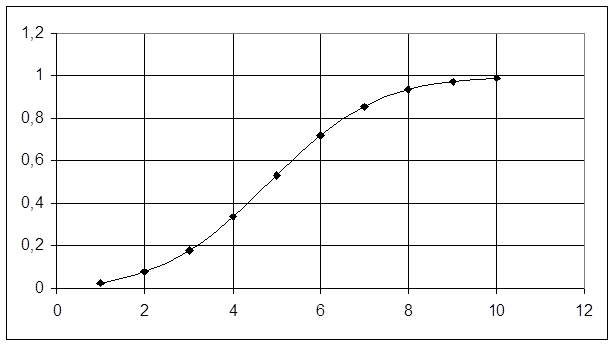
График функции распределения:

, , где L – принятая нами ширина графика, мм; .

График функции распределения на вероятностной бумаге:

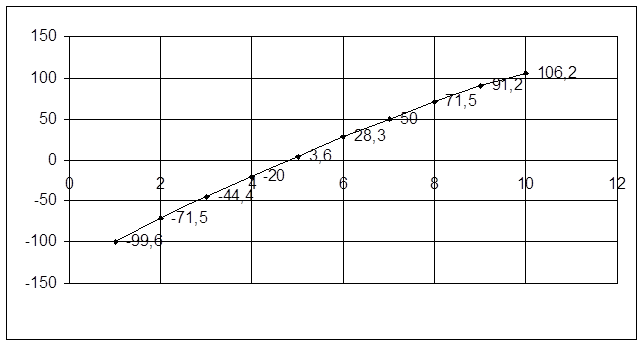
Вывод: В ходе выполнения работы была проведена проверка гипотезы о нормальном законе распределения статистических данных (в роли которых выступали резисторы номинальным сопротивлением 1 кОм). При проверке гипотезы о нормальном распределении был построен график функции распределения на вероятностной бумаге, все точки которого лежат на одной прямой. Величина критерия пирсона c²=3,307, полученная с помощью метода моментов, достаточно малая, а соответствующая ей вероятность P=0,986 > 0,8, значит гипотеза о нормальном законе распределения подтверждена.