Изучение методов обработки результатов пассивного эксперимента, построения математических моделей

1. Цель работы: изучение методов обработки результатов пассивного эксперимента, построения математических моделей, проверки адекватности модели.

2. Краткое содержание работы

1)  Построение математической модели;

2)  Проверка адекватности математической модели

3. Практическая часть

3.1. Исходные значения параметров

Исходные значения параметров приведены в таблице 1.

Таблица 1

3.2. Построение математической модели

Математическая модель строится в виде полинома, в нашем случае линейного:

, коэффициенты R₀ и a находятся по следующим формулам:

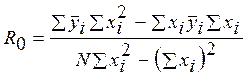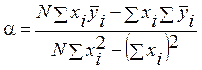, , где x_i –  значение температуры,  - математическое ожидание сопротивления.

В результате расчетов была получена следующая математическая модель:

3.3. Проверка адекватности модели

Поверка адекватности  модели проводится с использованием критерия Фишера:

.

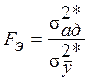Если F_э<F_т (при заданном уровне значимости p), то считается, что модель адекватна, в противном случае – не адекватна.

,  , ,   

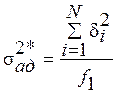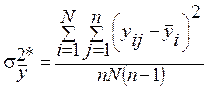где .

Рассчитанное значение F_э равно 3.2 , найденное по таблицам значение F_т равно 215,7. Видно, что построенная модель адекватна.

3.4. Проверка значимости коэффициентов

Считается, что коэффициент значим, если его абсолютная величина больше ошибки в его определении:

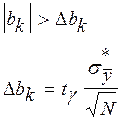
В данном случае при g=0,8,  t_g=1,31,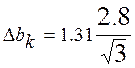

R₀: 109,288 > 0,85 – коэффициент значим

a: 0,0075 < 0,85 – коэффициент не значим

Графическая интерпретация полученных данных приведена на рис.1.

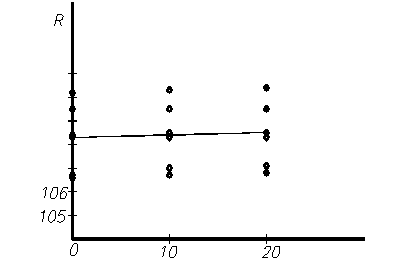
Рис. 1. График зависимости R от DT.

Вывод: в ходе лабораторной работы были изучены методы обработки результатов пассивного эксперимента, построения математических моделей, проверки адекватности модели. Была построена и проверена на адекватность модель зависимости сопротивления резистора от температуры.