Полная вероятность ошибки при различении двух сигналов

1.5. Полная вероятность ошибки при различении двух сигналов

Рассмотрим симметричную систему передачи двух сигналов: p₁=p₂=p, E₁=E₂=E . Пусть начальная фаза известна то есть сигнал детерминированный.

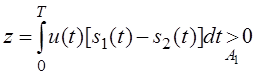
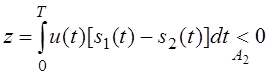
Где u(t)=s_i(t)+n(t),    i=1,2. Поэтому W(z) – нормальная плотность распределения вероятности. Каждый сигнал имеет свои характеристики – это

математическое ожидание – m, дисперсия - . Пусть передан сигнал s₁(t).           Тогда:

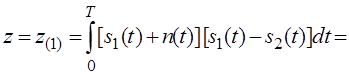
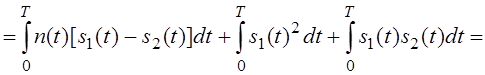
Учтём, что коэффициент взаимной корреляции:

                                                                

 

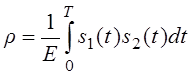
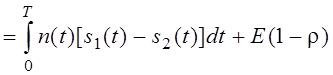
Найдём математическое ожидание – m₁ (первого сигнала):

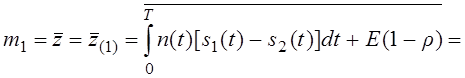
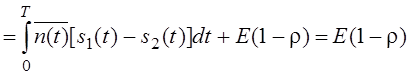
Так как    , то

        

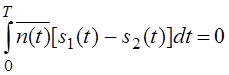
            То видно, что найдём дисперию –  (первого сигнала):

  ;       ;

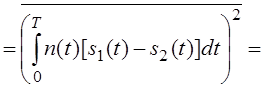
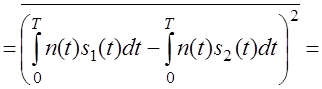
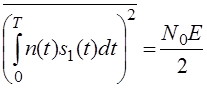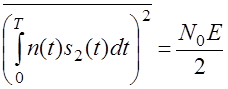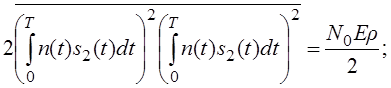
Аналогичную операцию проделаем для сигнала s₂(t). Пусть передан сигнал s₂(t). Тогда:

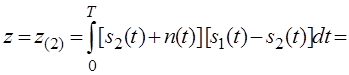
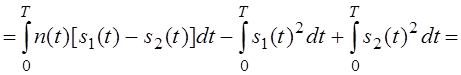
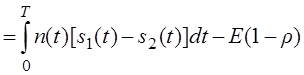
Найдём математическое ожидание – m₂ (второго сигнала):

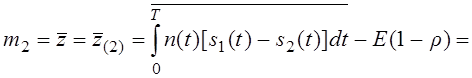
Проведя рассуждения аналогично как и с первым сигналом получим:

Найдём дисперию –  (второго сигнала):

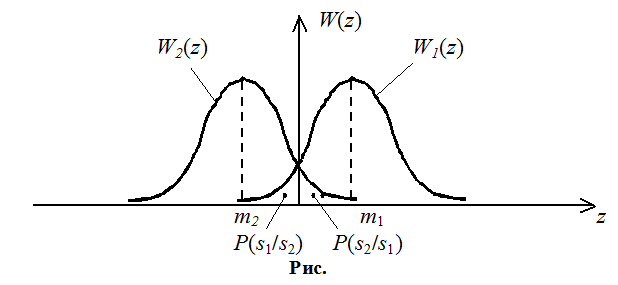
 Вероятность решения А₁, что передан сигнал s₁(t),

при условии что передан сигнал s₂(t).

        Вероятность решения А₂, что передан сигнал s₂(t),

при условии что передан сигнал s₁(t).

p₁=p₂=1/2

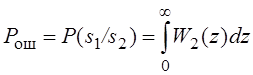
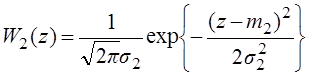
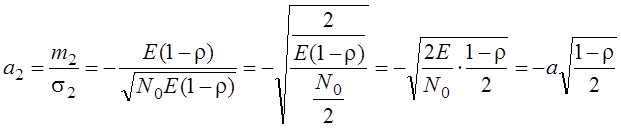
Где параметр :   

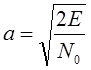
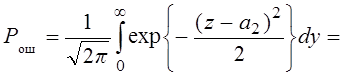
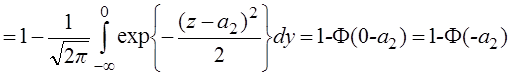
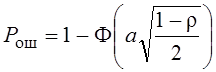
Пусть r=1  s₁(t)=s₂(t)        Р_ош = 1- Ф(0) = 1- 0,5 = 0,5 Одинаковые сигналы различить невозможно. m₁=m₂ =E(1-r)

Пусть r=-1 s₁(t)=-s₂(t)    Р_ош = 1- Ф(а)   значит сигналы оптимальные, сдвиг по фазе между сигналами составляет .

Пусть r=0 тогда сигналы будут ортогональны 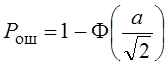. Чтобы добиться того же эффекта как и у r=-1 то необходимо: , а энергия сигналов должна быть в два раза больше =3 dB. Эти сигналы широко распространённые:

- Их сдвиг по фазе 

- Фазоманипулитованные сигналы

- Сигналы непрерывные по времени и по спектру

1.6. Различение М сигналов

С данной проблемой сталкиваются в радиотелеметрии. В каком-то интервале 0<t<T может быть передан один из М сигналов: s_i(t).где i=1,2,…,M.

u(t)= s_i(t)+n(t)  i=1,2,…,M.

Будем искать по критерию: , априорные вероятностиp_i=1/М,

где  i=1,2,…,M. Данному критерию характерно различае по максимальному правдоподобию.

Гипотезе Н_i соответствует сигнал s_i(t). Примем решение об различении такого сигнала для которого функция правдоподобия будет максимальной.

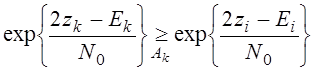
 при решении А_к .   Е_i=Е, где  i=1,2,…,M.

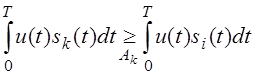 ,где  i=1,2,…,M

Различие сигналов проводится с помощью многоканальной схемы:

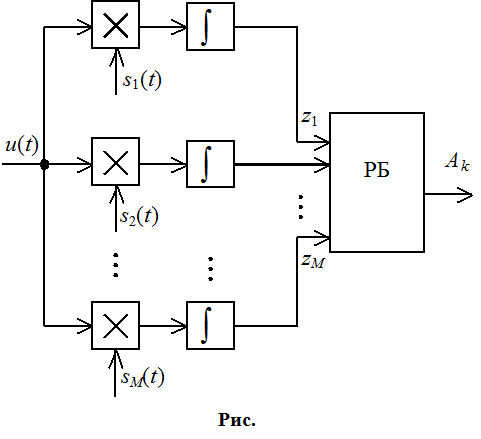
Различитель:

В каждом из i – сигналов определяется корреляция s_i(t) в виде корреляционного интеграла. Решение принимается решающим блоком, в котором корреляционный интеграл наибольший. Схему можно реализовать на основе СФ:

В каждом канале СФ (его импульсная характеристика  s_i( T-t ) ). Число каналов можно сократить на один, если в качестве опорного использовать разность синалов: s_i(t)-s₁(t)  i=2,3,..,M . Тогда будет разность корреляционных интегралов: Если z_i-z₁<0 то передавался сигнал s₁(t) [z_i>z₁].

Если

, где i=2,3,..,M

При передачи происходит перепутывание. Нужно найти Р_ош:

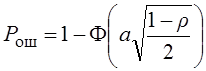,  где     :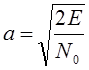

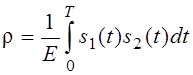
ЕслиM>2, то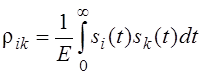 

считаем, что все сигналы равнокоррелированные  Е_i=Е  и .

Если передаётся сигнал s(t), то его можно перепутать с остальными (М-1) сигналами. Тогда полная Р_ош может возрасти в (М-1) раз, но не более.

1.7. Обнаружение М сигналов с неизвестной начальной фазой

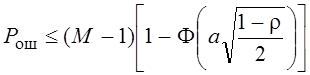
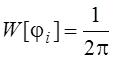   ;    - cлучайная величина

Функция провдоподобия находится усреднением по :

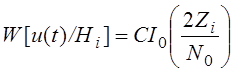,где  i=1,2,..,M

  ;        , гдеквадратурные составляющиекорреляционного интеграла, которые образуются на выходе СФ.                                                                    Правило максимального правдоподобия требует нахождения максимального значения функционала правдоподобия при различных i. I₀ - функция Бесселя (монотонная функция, по этому для различения можно использовать огибающую корреляционного интеграла).

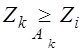 , где i,k=1,2,..,M

 Необходимо СФ и АД для вычисления огибающей:

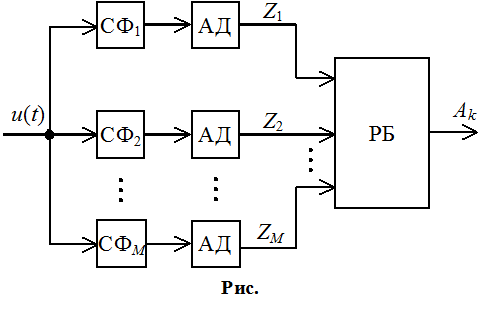
Решение принимается по параметру канала к о передачи сигнала s_k(t), в котором значение корреляционного интеграла максимально. Характеристика АД – может быть любой, но одинаковой для всех каналов. Сократить каналы нельзя так как используются нелинейные преобразователи – АД.