Выбор средств измерения линейных размеров

допускаемых погрешностей измерений и таблицей предельных погрешностей АСИ, выбираем средства измерения размеров детали.

Погрешностью измерения называется разность |ε-А| между результатом измерения ε и истинным значением измеряемой величины А.

Погрешность измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины (кроме случая настройки прибора).

Основной задачей обработки результатов измерения является оценка истинного значения измеряемой величины по полученным результатам, т.е. вычислить приближенное значение А с возможно меньшей погрешностью. За результат измерения А принимают среднеарифметическое результатов измерений А=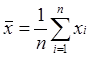, где n – число замеров; x_i – результат наблюдений.

Среднеарифметическое отклонение результата измерения δ оценивается по формуле δ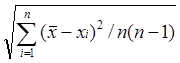₍₎=, а доверительный интервал случайной погрешности результата измерения при доверительной вероятности Р определяется величиной ε=kσ. Коэффициент k зависит от закона распределения результатов наблюдений и вероятности нахождения случайной погрешности в заданном интервале. Формы законов распределения случайных величин приведены в таблице. Наиболее распространенным при измерении линейных величин является закон нормального распределения.

При сравнительно небольшом числе измерений доверительные границы случайной погрешности результата измерения определяют по таблицам Стьюдента-Фишера по формуле ε=t₀ δ₍₎, где t₀ – коэффициент, установленный в зависимости от числа степеней свободы k=n-1 и заданной вероятностью Р.

Формы представления результатов измерений.

1.  А; Δ от Δ_н до Δ_в; Р, где А – результат измерения в единицах измеряемой величины; Δ, Δ_н и Δ_в – соответственно ПИ с нижней и верхней границами ее, в тех же единицах; Р – установленная вероятность, с которой ПИ находится в этих границах.

2.  А; Δ_с, Δ_сн, Δ_св; Р_с; (); f(ε), где Δ_с, Δ_сн, Δ_св – систематическая составляющая ПИ, нижняя и верхняя границы в единицах измеряемой величины; Р_с – заданная вероятность, с которой систематическая составляющая ПИ находится в этих пределах; () – оценка среднего квадратического отклонения случайной составляющей ПИ в единицах измеряемой величины; f(ε) – стандартная аппроксимация функции распределения случайной составляющей ПИ. Берется из перечня, приведенного в таблице.

3.  (Δ_с); f₀(ε); (); f(ε), где (Δ_с) – оценка предельного квадратического отклонения систематической составляющей ПИ в границах измеряемой величины; f₀(ε) – стандартная аппроксимация функции распределения систематической составляющей ПИ

4.  А; fΔ_с(ε); f(ε), где fΔ_с(ε) и f(ε) – функции распределения систематической и случайной составляющей ПИ, задаваемое таблицами, графиками, функциями