Определение функции нескольких переменных. Предел функции 2-х переменных, страница 4

=п∑(y_(i-1)+y_i) Опр. Число S= при Л_т->0 lim S(x), если при любом E>0 существует б(Е)>0 т.ч. при любом Т с Л_т<, => |S(x_i)-S| <E . Если существует конечный при Л_т->0 lim S(x_i), то поверх. назыв. квадрируемой и её площадь =S . Т. Пусть функ. Y=f(x) имеет на[a,b] непр. Производную f’(x) тогда S поверх. Вращения Sповерх.= 2п S(от а до b) f(x) (1+(f’(x))^2)^1\2 dx Если кривая задана параметрически то S=2п S(от α до в) y(t) ((x’)^2 +(y’)^2)^1\2 dt

36. ДУ высших порядков . Сведение их к нормальной системе.

-(2) ду n порядка разрешенное относительно старшей производной. х – независимая переменная у(х) – искомая функция

Решение (2)- функция у(х) , имеющая производные до n  порядка, которая обращает (2) в верное равенство пример: y’’’=x+5

Покажем что (2) сводится к нормальной системе

Решение (2) – Y(x) которая в D  имеет частные производные до n  порядка, (x,y,y⁽¹⁾ ….y⁽ⁿ⁾)

принадлежит D  и обращает данное Ур-е в тождество.

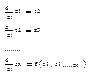Рассмотрим нормальную систему где f – тоже функция, которая стоит в правой части (2)

] Y(x) – некоторое решение (2), построим функции z1(x)=y(x) … zn(x)= y^(n-1)

Y(x)=z1(x) –решение (2) т.е.  y⁽ⁿ⁾= (x,y,y⁽¹⁾ ….y^(n-1)) сводится к нормальной системе.

Задача Коши

Пусть  z0 – начальное условие для задачи Каши в нормальной системе.

Решение системы для нормальной системы соответствует решению задачи Каши с указанными нормальными уравнениями, причем задается сама функция  в точке и все ее производные до n-1 порядка.

Теорема:

Если f(x,y,y⁽¹⁾ ….y^(n-1)) непрерывна  на (а,b) вместе со своими частными производными по переменным y, y’ … y^(n-1)  то существует решение Y(x)  на (a,b) удовлетворяющее условиям y(x0)=y0…. y^(n-1)(x0)= y0^(n-1)

41.Линейные ДУ с постоянными коэффициентами n-го порядка.

L(y)=f(x)

L(y) – n-ая производная y^(n)+q1*y^(n-1)+…+qn*y

Пусть f(x)=0 => уравнение однородное.

Решение ищем в виде y=e^(kx).

y^n=e^(kx)*(k^n+q1*k^(n-1)+…+qn)=0

k^n+q1*k^(n-1)+…+qn=0 – характеристическое уравнение, у которого слева многочлен степени n => многочлен имеет n корней с учетом кратности =>

Пусть многочлен имеет l различных корней, кратность которых – rk =>

(k-k1)^r1*(k-k2)^r2…(k-ke)^re=0. k1-корень кратности r1.

Пусть k1 – корень кратности r1. r1+r2+…+re=n

=> y1=e^(k1x) (1ое решение) и если корень кратности r1, то y2=x*e^(k1x) тот и т.д

yn=x^(r1-1)*e^(k1x) тоже решение. Аналогично с другими корнями.

Если среди корней есть комплексный корень k, то k- тоже корень.

e^(kx),e^(x)-решение однородного уравнения

V1=(e^(kx)+e^(x))/2   V2=(e^(kx)-e^(x))/2i – тоже решение, которым соответствует решение y=e^(x)(cosx+sinx) из формул Эйлера уже выводили.

Если кратность корня>1 (r>1) ,то y=x^(r-1)* (cosx+sinx)- тоже решение , где y1…yn - фундаментальная система решений.

№8Физическое приложение определенного интеграла . Первая теорема Гульдена . 1) Вычисление массы стержня. Рассм. Неоднор. Стержень , расположенный на [a,b] оси ОХ. Пусть р(х) линейная плотность  р(х)=при ⌂x->0 lim (m(x+⌂x)-m(x) ) / ⌂x где m(x+⌂x)-(x) –масса стержня на [x,x+⌂x] . T: a=x₀<x₁<…<x_n=b ⌂x=x_i-x_(i-1) . Л_т=max ⌂x_i  выберем точку C_i принадлежащую (x_(i-1),x_i) . m=∑ p(C_i) *⌂x_i ;  m=при Лт->0 lim =∑ p(Ci) ⌂xi = S(от a до b) p(x) dx  2) Вычисление статических моментов координат центра тяжести  кривой и плоской обл. Рассм. На плоск систему матер. Точек с координатами mi и направленную ось. Статическим моментом точек относ. Оси l назыв =∑ m_i*d_i где d_i расстояние от i-ой точки до оси l, взятое с + если точки расположены по левую от l  и с – если по правую сторону . Точка М назыв. Центром тяжести системы материальных точек , если после помещения в эту точку шарика массой m1+m2+m3+…+mn статический  момент этой точки относ. Любой оси совпадает со стат. Моментом всей системы. Рассм. На плоск. Кривую L: x=x(t) y=y(t) α <=t<=в T: α=t0<t1<t2<….<tn=в . На кривой получим т точки Мi(x(ti),y(ti)) . Пусть лин. Плотность р=1 тогда m=S(от α до в) ((x’)^2+(y’)^2)^1/2 dt ; li= l_M(i-1)*Mi = l(ti) –l(t(i-1)) = (по Т Лагранжа) = l’(ci)*⌂ti= ((x(ci))^2+(y(ci))^2)^1/2 *⌂ti . Статический момент относ Ох Mx= ∑ y(ci)*li= ∑y(ci)* ((x’(ci))^2+(y’(ci))^2)^1/2 *⌂ti ; Mx-=S(от a до b) y(t) *((x’)^2+(y’)^2)^1/2 dt .Статический момент этой кривой относ. Оy: My=(от a до b) x(t) *((x’)^2+(y’)^2)^1/2 dt . Координаты центра тяжести P(ξ,h). ξ= My/m=My/l ; h=Mx/m=Mx/l; => hl=My , 2пhl=2п S(от a до b) y(t) *((x’)^2+(y’)^2)^1/2 dt это 1-я теорема Гульдена.