















![]() 3.2 ПРИМЕНЕНИЕ
АППАРАТА ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ГАЛЛЕНОВСКОГО ТИПА ДЛЯ РАСЧЕТА ЭЛЕКТРОДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ДИРЕКТОРНЫХ АНТЕНН
3.2 ПРИМЕНЕНИЕ
АППАРАТА ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ГАЛЛЕНОВСКОГО ТИПА ДЛЯ РАСЧЕТА ЭЛЕКТРОДИНАМИЧЕСКИХ
ХАРАКТЕРИСТИК ДИРЕКТОРНЫХ АНТЕНН
Директорная антенна, или антенна типа «волновой канал», часто называемая именем ее изобретателя – антенна Уда-Яги, образуется из проволочных вибраторов, располагаемых параллельно в одной плоскости. Один из вибраторов является активным, а остальные – пассивными, из которых один из вибраторов, располагаемый позади активного, играет роль рефлектора, а остальные, располагаемые впереди активного вибратора, играют роль директоров.
Из теории
связанных вибраторов известно, что пассивный вибратор является рефлектором,
если его реактивное сопротивление имеет индуктивный характер. По этому длина
рефлектора берется несколько больше ![]() .
.
Пассивный вибратор
становится директором в том случае, если имеет емкостную реактивную часть
входного сопротивления. По этому длину директоров берут несколько меньше ![]() .
.
В качестве рефлектора используют обычно только один вибратор, так как последующие рефлекторы слабо возбуждаются и не оказывают существенного влияния на излучение антенны, но для широкополосных директорных антенн рационально использовать составной рефлектор. Количество же директоров может быть большим, поскольку излучение антенны направлено в сторону директоров и, в следствии этого, они последовательно и довольно интенсивно возбуждаются, образуя «волновой канал» с замедленной волной. Энергия, распространяющаяся по волновому каналу, образованному директорами, доходя до конца (до последнего директора), частично отражается. В результате в волновом канале, образованном директорами, как и в обычном волновом канале, образуется падающая и отраженная волны. В этом отношении директорная антенна аналогична антеннам бегущей волны, широко применяемым в области коротких волн.
При надлежащей
настройке директоров амплитуда отраженных волн становится весьма малой. Четкой
теории в отношении размеров директорных антенн не существует, поэтому при конструировании
антенн такого типа необходимо использовать опыт предыдущих разработчиков и эксперимент.
Исходя из этого, расстояние между активным вибратором и рефлектором берется в
пределах (0,15 – 0,25)![]() , а между активным вибратором
и первым директором, а также между соседними директорами – в пределах (0,1 –
0,35)
, а между активным вибратором
и первым директором, а также между соседними директорами – в пределах (0,1 –
0,35)![]() .
.
В качестве активного вибратора директорной антенны обычно применяют петлевой вибратор. Это объясняется следующими причинами. В директорной антенне благодаря влиянию пассивных вибраторов сопротивление активного полуволнового падает до 20-30 Ом, что затрудняет согласование с питающим фидером. Входное сопротивление петлевого вибратора равно примерно 290 Ом. И поэтому при настройке остается довольно большим. Петлевой вибратор обладает лучшими диапазонными свойствами и его можно непосредственно крепить к несущей конструкции в точке нулевого потенциала. Изоляторы для крепежа в этом случае не нужны.
Из выше изложенного вытекают достоинства директорных антенн:
![]() простота и прочность конструкции;
простота и прочность конструкции;
![]() удобство в возбуждении большого числа
вибраторов.
удобство в возбуждении большого числа
вибраторов.
Недостаток – ограниченность рабочего диапазона.
Исходя из изложенного выше, директорная антенна представляет собой совокупность определенным образом соединенных, прямолинейных проводников (все округления заменяются прямыми), для которой можно использовать аппарат модифицированных систем интегральных уравнений Галленовского типа трехмерной антенной структуры, состоящей из прямолинейных проводников. Упрощенная модель директорной антенны представлена на рис. 4, на нем учтены симметричные свойства антенны.
Рассмотрим
систему, состоящую из N прямолинейных,
произвольно ориентированных проводников. На рис. 5 показано размещение двух
элементов этой системы. Будем считать, что проводники возбуждаются сторонним
электрическим полем напряженностью ![]() . Это может быть
поле падающей на систему плоской волны или поле сосредоточенного источника.
Проводники системы обладают некоторым поверхностным импедансом
. Это может быть
поле падающей на систему плоской волны или поле сосредоточенного источника.
Проводники системы обладают некоторым поверхностным импедансом ![]() . Свяжем с каждым из рассматриваемых
элементов прямоугольную систему координат
. Свяжем с каждым из рассматриваемых
элементов прямоугольную систему координат ![]() ,
таким образом, что орт
,
таким образом, что орт ![]() совпадает с осью
проводника,
совпадает с осью
проводника, ![]() образуют вместе с
образуют вместе с ![]() правую тройку векторов.
правую тройку векторов.
Расстояние между
точками наблюдения ![]() и интегрирования
и интегрирования ![]() в рамках тонкопроволочного
приближения определяется следующим соотношением:
в рамках тонкопроволочного
приближения определяется следующим соотношением:
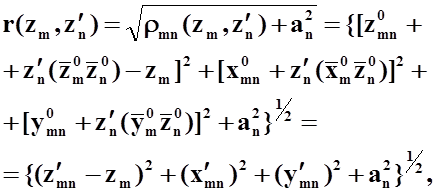 (20)
(20)
где ![]() - проекции вектора
- проекции вектора ![]() на оси m-ой системы координат,
на оси m-ой системы координат, ![]() -радиус n-го проводника.
-радиус n-го проводника.
Напряженность электрического поля, созданная в точке наблюдения токами, протекающими по проводнику, определяется известной формулой:
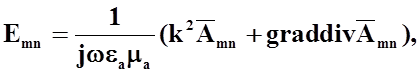 (21)
(21)
где ![]() - векторный потенциал, создаваемый n-м элементом на поверхности m-ого;
- векторный потенциал, создаваемый n-м элементом на поверхности m-ого;
![]() - круговая частота;
- круговая частота;
![]() ,
,![]() -
диэлектрическая и магнитная проницаемости;
-
диэлектрическая и магнитная проницаемости;
![]() - волновое число.
- волновое число.
В рамках обычно используемого приближения для тонких проводников векторный потенциал может быть найден по формуле:
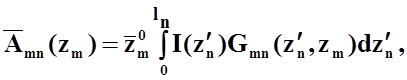 (22)
(22)
где ![]() - ток n-ого элемента системы;
- ток n-ого элемента системы;
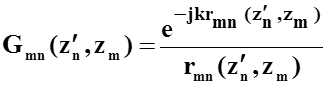
В формуле (22) точки интегрирования находятся на оси излучателя, а точка наблюдения находится на его поверхности.
Обозначим через ![]() векторный потенциал на поверхности m-ого проводника,
создаваемый всеми проводниками системы. Проекции вектора
векторный потенциал на поверхности m-ого проводника,
создаваемый всеми проводниками системы. Проекции вектора ![]() в декартовой системе координат примут
вид:
в декартовой системе координат примут
вид:
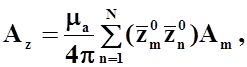
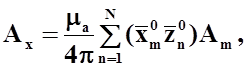
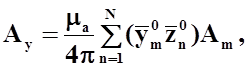 (23)
(23)
где 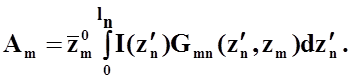
В соответствии с формулой (21) для касательной составляющей напряженности электрического поля на поверхности m-ого проводника, получим следующее выражение:
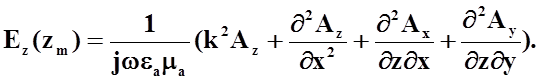
Удовлетворяя граничным условиям на поверхности проводника с распределенным поверхностным импедансом, получим:
![]() (24)
(24)
где ![]() - сопротивление единичного отрезка
проводника, определяемого соотношением:
- сопротивление единичного отрезка
проводника, определяемого соотношением:
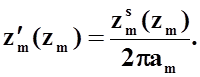
Следовательно, для
векторного потенциала ![]() найдем следующее соотношение:
найдем следующее соотношение:
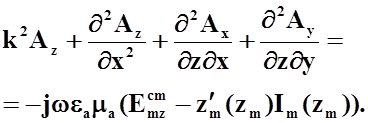 (25)
(25)
Выражение (25) можно рассматривать как неоднородное дифференциальное
уравнение второго порядка относительно функции ![]() .
Решение этого уравнения представим в виде суммы общего решения однородного
уравнения и какого-либо частного решения неоднородного уравнения. Общее решение
однородного уравнения, очевидно, имеет вид:
.
Решение этого уравнения представим в виде суммы общего решения однородного
уравнения и какого-либо частного решения неоднородного уравнения. Общее решение
однородного уравнения, очевидно, имеет вид:
![]()
где ![]() ,
,![]() -
неизвестные комплексные постоянные.
-
неизвестные комплексные постоянные.
Частное решение неоднородного уравнения представим в виде интеграла:
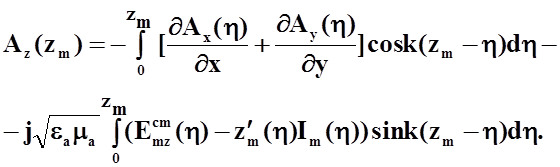
Справедливость такого представления нетрудно проверить непосредственной подстановкой. Таким образом,
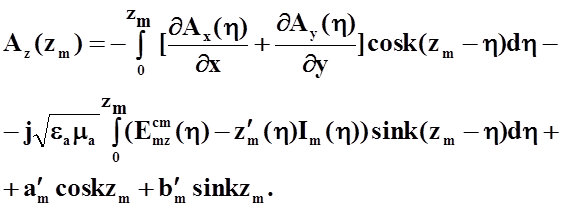 (26)
(26)
С использованием уравнения калибровки
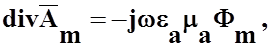 (27)
(27)
которое связывает
скалярный потенциал ![]() и векторный потенциал
и векторный потенциал ![]() , соотношение (26)принимает следующий вид:
, соотношение (26)принимает следующий вид:
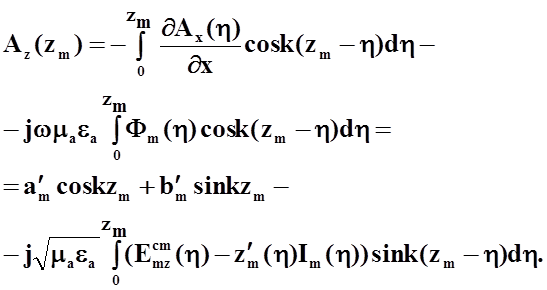 (28)
(28)
Известно, что скалярный потенциал системы проводников определяется формулой:
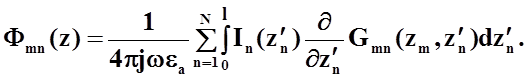 (29)
(29)
Подставляя (29)в (28), и учитывая (23) , получим:
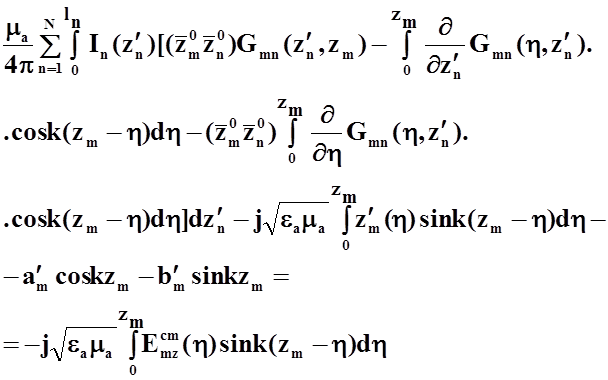 (30)
(30)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.