Применение аппарата интегральных уравнений галленовского типа для расчета электродинамических характеристик директорных антенн, страница 2

Последнее соотношение можно рассматривать как интегральное уравнение для неизвестной функции тока . Ядро уравнения (30) содержит операцию интегрирования производной функции Грина . Следовательно, при численном решении возникает необходимость вычисления двойных интегралов. Эти обстоятельства вызывают значительное увеличение затрат машинного времени, снижают точность решения задачи, делают уравнения  (30) неэффективными для сложных многоэлементных излучателей. Однако в рассматриваемой задаче для систем, состоящих, из прямолинейных проводников, структуру ядра можно существенно упростить, тем самым в значительной степени ослабить отмеченные недостатки. Подробное изложение процедуры преобразования ядра интегрального уравнения (30) приведено в [1]. Проделав аналогичные преобразования, получим следующее интегральное уравнение:

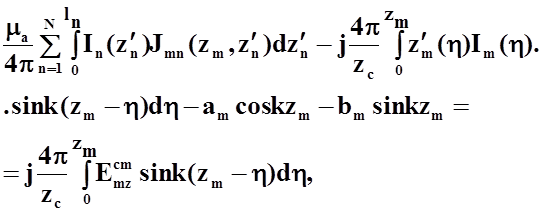      (31)

где  - ядро интегрального уравнения. Здесь - координатная функция, зависящая от ориентации системы координат m-ого элемента и имеющая вид:

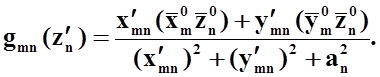
Она имеет наиболее простую форму, если выполняется соотношение , , что всегда можно добиться вращением системы координат m-ого элемента вокруг оси . В этом случае имеет вид:

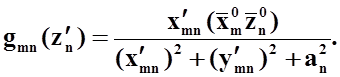
Уравнение (31) является предпочтительным в вычислительном отношении, поскольку имеет более простой вид ядра.

Если проводники рассматриваемой системы имеют между собой соединения (рис. 6), то необходимо обеспечивать непрерывность скалярного потенциала в местах соединения проводников, что приводит к следующим уравнениям, именуемыми в дальнейшем «потенциальными»:

                                                         (32)

где и координаты точки соединения p-ого и q-ого проводников в соответствующих им системах координат. Выражение для функции скалярного потенциала может быть найдено из уравнения (31)для продольной составляющей векторного потенциала:

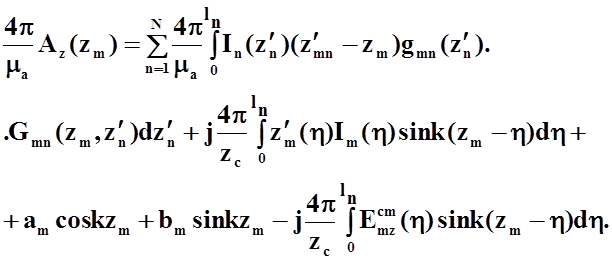  (33)

С использованием уравнения калибровки (27)соотношение(33)преобразуется к виду:

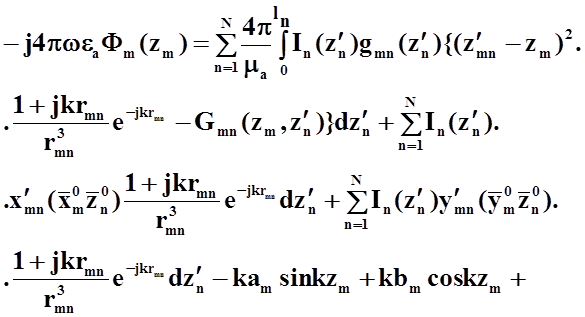
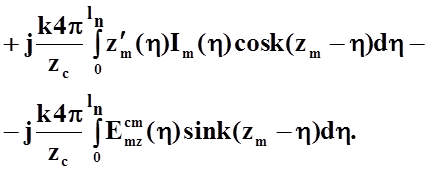
Упростив последнее выражение, получим:

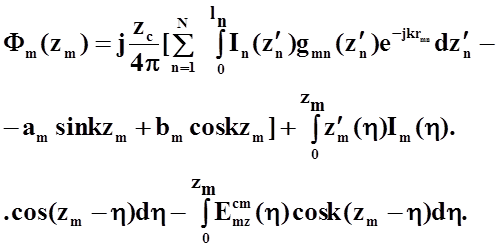             (34)

Подставляя  выражение (34)в(32)получаем следующий вид потенциального уравнения:

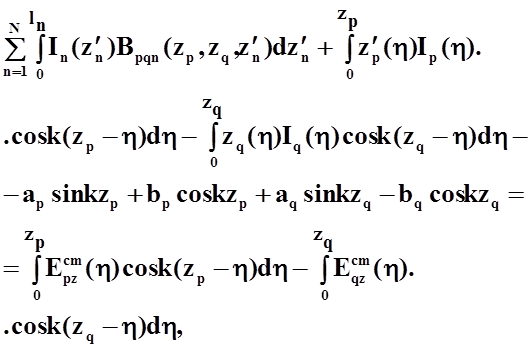         (35)

где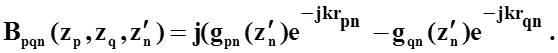

Таким образом, соотношения (31) и(35) позволяют построить систему интегральных уравнений для рассматриваемой системы произвольным образом  ориентированных и соединенных тонких прямолинейных проводников с распределенным поверхностным импедансом.

Во многих случаях, часто встречающихся в практических приложениях, антенна располагается в близи поверхности плоского металлического экрана. Именно в таких условиях находятся антенны, исследуемые в настоящем проекте. Для упрощения теоретического анализа считают, что экран представляет собой идеально проводящий () металлический лист бесконечных размеров, при этом ядра интегральных уравнений (31)и(35)с учетом зеркальных изображений примут следующий вид:

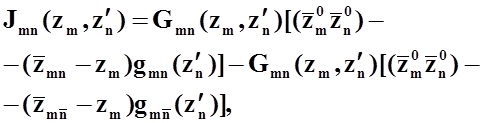                          (36)

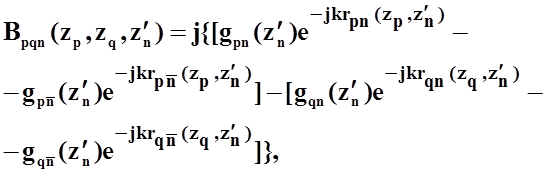               (37)

где - индекс, соответствующий зеркальному изображению n-ого проводника. Интегральные уравнения (31)и(35)с ядрами вида(36)и(37)можно использовать и для нахождения токов в антеннах, расположенных в свободном пространстве, но имеющих зеркальную симметрию. При этом размерность задачи сокращается в два раза.

Интегральные уравнения (31) и(35) получены для произвольного возбуждения системы проводников сторонним электрическим полем . Это может быть, как отмечалось, поле плоской волны, падающей на систему проводников с произвольного направления. По найденному из решения системы интегральных уравнений распределению токов в проводниках легко определить в этом случае и характеристики рассеивания проволочной структуры.

Предметом настоящего проекта является нахождение электродинамических характеристик проволочных антенн, возбуждаемых сосредоточенными источниками (генераторами). Истинное распределение сторонних полей сильно зависит от конструкции узла питания и зачастую не поддается строгому математическому описанию. Поэтому при теоретическом анализе антенн часто применяют идеализированные модели возбуждающих устройств: в виде дельта-функции Дирака, кольца магнитного тока, тонкой щели. В дециметровом и более низкочастотных диапазонах, где расстояния между точками провода, к которому подключается сторонний источник возбуждения, мало по сравнению с длинной волны, широкое распространение получила модель дельта-генератора. В рамках этой модели поле в разрыве проводников считается постоянным и не участвующим в излучении антенны, а величина его определяется разностью потенциалов между точками включения источника, и может быть представлена в виде:

                                             (38)

где - точка включения стороннего источника возбуждения.

Учитывая представления источника в виде (38)правая часть уравнения (31) запишется в виде:

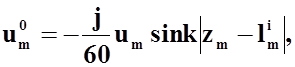                             (39)

где - напряжение источника возбуждения, подключаемого к m-ому проводнику на расстоянии от начала его системы координат, а правая часть потенциального уравнения (35) , соответственно примет вид:

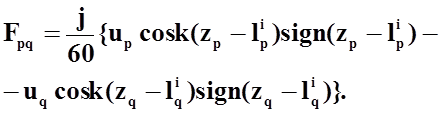                  (40)

Смысл величин, входящих в это соотношение, тот же, что и в выражении (39).

Модель дельта-генератора имеет некоторые особенности для различных интегральных уравнений. Наиболее подходящей моделью для интегральных уравнений Мея является именно эта, так как при этом правая часть представляет собой гладкую функцию. Уравнения Мея не критичны к модели источника возбуждения, чего нельзя сказать об уравнениях Поклингтона. С учетом сделанных замечаний система модифицированных уравнений Галленовского типа имеет следующий вид:

      

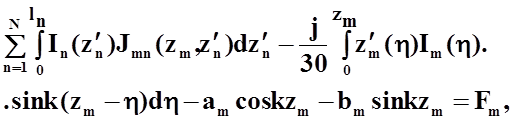
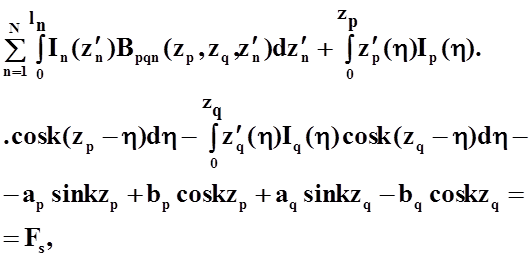           (41)

где  и - ядра интегральных уравнений, определяемые, соответственно, выражениями (36)и(37), а и выражениями(39)и(40). Соответствиеp,qиs задается таблично, для каждой конкретной системы проводников.

Таким образом, полученная система интегральных уравнений содержит Nуравнений, удовлетворяющих граничным условиям для касательной составляющей напряженности электрического поля на поверхности проводников, а такжеP уравнений, обеспечивающих выполнение равенств скалярных потенциалов в местах соединения проводников. Количество потенциальных уравнений определяется количеством соединений проводников и выражается следующей простой зависимостью:

 

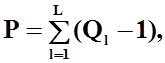
где  - количество проводников, сходящихся в l-том узле,L – количество узлов (точек пересечения, соединения проводников) в рассматриваемой системе. В заключении этого подраздела отметим, что полученное интегральное уравнение (31) представляет собой дискретный аналог уравнения Мея. Однако выгодно отличается от него отсутствием в ряде операций интегрирования производной функции Грина. Кроме того, ядро уравнения (31) для тонкопроволочного приближения содержит лишь интегрируемую часть, пропорциональную величине . Эти обстоятельства упрощают численную реализацию метода, делая его чрезвычайно эффективным в вычислительном отношении.