Метод координат в классах с углубленным изучением математики.
С методом координат в пространстве учащиеся знакомятся в курсе геометрии 11 класса. После ознакомления с прямоугольной системой координат, учащиеся выводят уравнение плоскости по точке и нормальному вектору. Математическим аппаратом при этом является скалярное произведение векторов.
Доказывается теорема: Всякое уравнение I степени ax+by+cz+d=0 относительно текущих координат есть уравнение плоскости, нормальным вектором которой является вектор n(a, b, c).
Пусть
a: ax+by+cz+d=0 – уравнение некоторой поверхности. Возьмем
произвольную точку 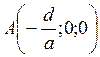 при
при ![]() .
Составим уравнение плоскости
.
Составим уравнение плоскости 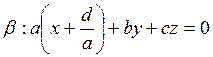 ,
, ![]() поверхность совпадает с плоскостью,
следовательно
поверхность совпадает с плоскостью,
следовательно ![]() - уравнение плоскости.
- уравнение плоскости.
б) Различные случаи расположения плоскости.
d=0 ![]() Þ О(0;0;0) Î a
Þ О(0;0;0) Î a
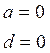
![]() проходит
через Ох
проходит
через Ох
![]() проходит через Ох
проходит через Ох
![]() || Ох
|| Ох
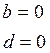
![]() проходит
через Оу
проходит
через Оу
![]()
![]() || Оу с=0
|| Оу с=0
![]() проходит через Oz
проходит через Oz
![]() || Oz
|| Oz
Учащиеся должны уметь выводить уравнение плоскости по трем точкам. С этим заданием желательно познакомить учащихся через конкретную задачу. Из всех способов решения самым рациональным является следующий.
Задача. Даны три точки А(1;2;3), В(2;2;2) и С(1;3;3). Записать уравнение плоскости (АВС).
Решение.
1.
Пусть нормальный вектор ![]() имеет координаты:
имеет координаты: ![]() .
Тогда он будет перпендикулярен векторам АВ и АС.
.
Тогда он будет перпендикулярен векторам АВ и АС.
![]() ,
, ![]() .
.
2. 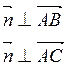
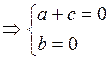
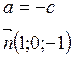
3. Составим уравнение плоскости (АВС) по точке А и нормальному вектору:
![]()
![]() ;
; ![]()
Получим формулу для нахождения расстояния от точки до плоскости.
Задача. Даны плоскость a: ax+by+cz+d=0 и точка А(x0;y0;z0). Найти расстояние от точки до плоскости.
Решение.
|
|

|
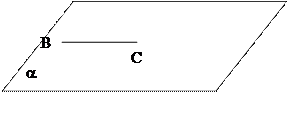 |
Возьмем произвольную точку В плоскости a.
Пусть
![]() , тогда
, тогда ![]() , т.е.
, т.е. ![]() ;
;
![]() , где
, где ![]() - угол
между векторами
- угол
между векторами ![]() и
и ![]() .
.
В
треугольнике АВС: ![]() , тогда
, тогда ![]()
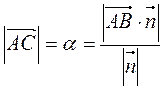 ; (1)
; (1)
подставим в формулу (1) координаты, получим:
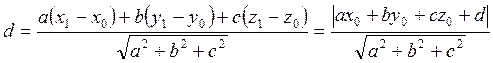
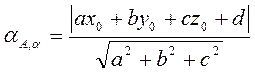
Учащиеся выводят уравнения прямых: а) по точке и направляющему вектору;
б) по двум точкам;
в) параметрические уравнения прямой.
Затем рассматривается взаимное расположение прямых:
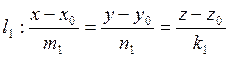 1)
1) 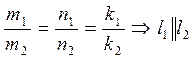
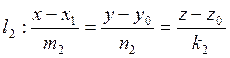 2)
2) ![]()
![]()
|
|
 3)
3) 
![]()
![]() 4)
4) ![]()
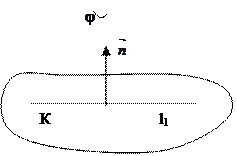 |
![]()
![]()
d
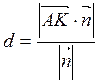 (2)
(2)
Задача:
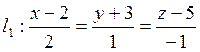
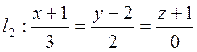
Найти
расстояние между прямыми ![]() и
и ![]() .
.
Алгоритм решения задачи:
1. Найдем нормальный вектор ![]() для
для
![]() и
и ![]()
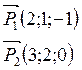
![]()
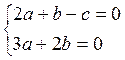
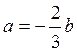
![]() ,
, ![]() ,
, ![]()
![]()
Найдем расстояние между прямыми по формуле (1).
2. ![]()
![]()
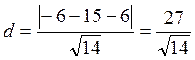
![]()
Т.к.
прямые ![]() и
и ![]() не
параллельны и расстояние не равно нулю, то эти прямые скрещивающиеся.
не
параллельны и расстояние не равно нулю, то эти прямые скрещивающиеся.
Затем учащиеся выводят уравнение сферы, уравнение (неравенство) шара.
Задание фигуры в пространстве Ф(x,y,z)=0
Знакомятся с другими системами координат:
 |
|||||||
 |
|||||||
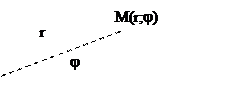 |
|||||||
|
|||||||
|
|
|
 |
цилиндрические координаты
Сферические координаты: географические (широта, долгота)
сферические координаты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.