Значение и место изучения показательной и логарифмической функций, страница 4

Областью изменения функции , заданной на множестве R, является множество ; её графиком является кривая линия, которой принадлежат все точки графика показательной функции с областью определения Q; называют её показательной функцией на множестве R. Тем самым допускается, что степени с иррациональным показателем имеют смысл. При закреплении следует выполнить упражнения вида:

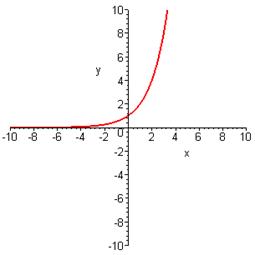
1)  Построить график функции при а=3 и по её графику найти:

а) значение y при x=0,5; 1,4; -1

б) значение x при y=0,5; 1,4; 1,7

2) Пользуясь графиком функции, заданной формулой , представить, если это возможно, числа -1,5; -1; 0; 1; 1,2 в виде степени с основанием 3.

На ранее рассмотренных и этих примерах учащиеся должны подойти к следующему определению показательной функции:

- функция, которую можно задать формулой вида  где x иy– переменные, а – положительное число, называется показательной.

Аналитическое и графическое исследование показательной функции должно так же проводиться во взаимной связи. Так, до построения графика функции можно установить наличие нулей, наибольшего и наименьшего значений, промежутков знакопостоянства и монотонности функции. А затем построить график и дать этим свойствам графическую интерпретацию и с помощью графика установить и другие свойства показательной функции. Учащиеся должны уметь строить графики функций и по ним формулировать следующие основные свойства:

·   - область определения функции;

·   - область значений функции при , {1} - область значений функции при а=1;

·  Функция при а>1- возрастающая, при 0<а<1 – убывающая, при  а=1 – монотонна;

·  При x=0 значение функции равно 1;

·  При а>1: если x>0, то  и если  x<0, то .

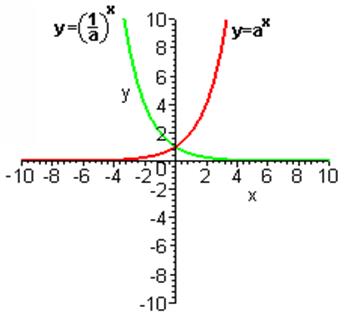
По всем перечисленным свойствам, кроме свойства 2 при , учащиеся должны уметь проводить аналитические обоснования на случая множества Q на основе определений и свойств степеней с целыми и дробными показателями. Кроме того, учащиеся должны уметь пользоваться тем, что графики показательных функций с  и  симметричны относительно оси ординат. С этой целью выполнять упражнения вида:

- Постройте графики и исследуйте функции, заданные формулами:

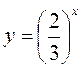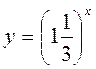а) и;   б) и

Раскрытию широких применений показательной функции будет способствовать знакомство учащихся с тем, что любая геометрическая прогрессия является функцией, заданной формулой  на множестве натуральных чисел.

п. 1.2 Показательные уравнения и неравенства.

При изучении главы «Показательная функция» учащиеся знакомятся со следующими типами показательных уравнений и неравенств:

1. Показательные уравнения:

а) Уравнения вида

На основании определения степени с нулевым показателем решение уравнения   сводится к уравнению , где f(x) – функция, определённая на множестве R. Решая последнее уравнение относительно x, найдём корни уравнения, удовлетворяющие уравнению . Верно и обратное: если выполняется равенство , то выполняется равенство .

Пример:

Решение: По определению степени с нулевым показателем:  : x²-5x+6=0, откуда x₁=2, x₂=3.   Ответ: {2;3}.

б) Уравнения вида:

Левая и правая части уравнения  приведены к одному основанию. В этом случае решением уравнения такого типа будут корни уравнения . Действительно, разделив уравнение на ,  где , получим 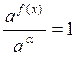, или , откуда следует, что , .

Пример: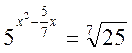

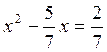Решение: Так как , то  и  

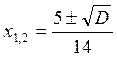 ,  D= 25 + 56 = 81   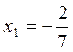и

Ответ: {; 1}.