Значение и место изучения показательной и логарифмической функций, страница 3

Вывод: , то есть f – возрастающая.

После чего учащимся сообщить, что в дальнейшем будем рассматривать функции, заданные формулой , только при a>0 и что они называются показательными функциями. Закрепление нужно провести на таких упражнениях:

-Например, исследовать функцию, заданную формулой:

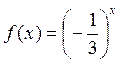а) ;     б) , где .

Определение степени с положительным основанием и дробным показателем небходимо ввести следующим образом:

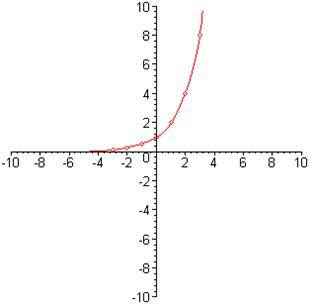- Строится график показательной функции, заданной формулой  , на множестве целых чисел.

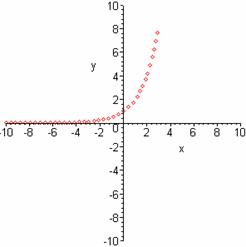
- Замечаем, что график функции состоит из отдельных точек, абсциссы которых есть целые числа, и что точки располагаются по некоторой плавной кривой. Проведя эту линию, надо убедиться, что она является графиком некоторой новой функции, например f,  которая определена на множестве всех чисел. По графику функции f  найти её значения при . Например, 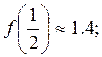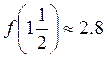;  и др. Затем обратить внимание учащихся на то, что значения функции fдля  могут быть найдены по формуле . Если предположить, что и для нецелых  значений xможно находить соответствующие значения функции f  по формуле , то следует считать, что   и так далее. Но такие выражения не имеют смысла, так как понятие степени пока определено для целого показателя. Чтобы этим выражениям придать смысл, расширим понятие степени на случай с дробным показателем, определив степень с дробным показателем.   

Будем исходить, что и для любого показателя сохранилось основное свойство степени  с целым показателем: . Тогда например, , то есть 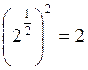, кроме того  по графику функции f. Но положительное число, квадрат которого равен двум, есть арифметический квадратный корень из числа 2. Поэтому можно считать , кроме того и по графику найдено 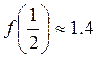. То есть целесообразно приписать следующий вывод: .

На основе вышеприведенных рассуждений ввести следующее определение:

- Если а>0 и х – произвольное дробное число, представленное дробью , где m - целое n – натуральное, то .

После чего отдельно ввести ещё одно определение:

- Если а=0 и х – дробное положительное число, то

Рассмотрев свойства степени с рациональным показателем и достаточно поупражнявшись в их тождественных преобразованиях перейти к исследованию показательной функции с областью определения Q.

Затем до построения графика при некоторых значениях а провести доказательство следующих свойств показательной функции:  

1.  функция принимает только положительные значения;

2.  функция является возрастающей при а>1;

3.  функция является убывающей при 0<а<1;

4.  функция не монотонна при а=1.

Данные свойства доказать, опираясь на определения и свойства степеней с целым и дробным показателями. Например, можно провести доказательство свойства 2. при а=2 так:

Дано:

Доказать: f – возрастающая.

Доказательство:

1.   и .

2.  f – возрастающая, если для любых значений аргумента из

3. 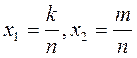 , где

4. 

5.   и  - по определению степени с дробным показателем.

6.  , так как функция возрастает при а>1.

7.  , так как функция вида - возрастает.

8.   - по определению степени с дробным показателем.

Итак, f – возрастающая.

Теперь можно перейти к построению графика показательной функции на множестве рациональных чисел, где сообщить учащимся о существовании монотонной функции на множестве действительных чисел; её можно задать формулой вида , где а>0.