Уметь проводить доказательство
монотонности степенной функции, заданной формулой ![]() с
натуральным показателем при
с
натуральным показателем при ![]() - аналитически давать
графическую иллюстрацию:
- аналитически давать
графическую иллюстрацию:
Дано: ![]()
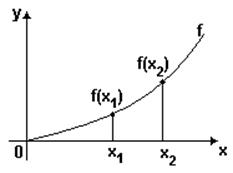 Доказать: f – возрастающая.
Доказать: f – возрастающая.
Доказательство:
f – возрастающая, если: ![]()
![]() , то
есть:
, то
есть: ![]() ,
, ![]()
![]()
Аналогичные требования предъявляются
к усвоению учащимися свойств корней n-й степени и арифметического корня. Так, из тождества ![]() при
при ![]() учащиеся уметь выводить следующие
свойства корня n-й степени:
учащиеся уметь выводить следующие
свойства корня n-й степени:
1) ![]()
2) 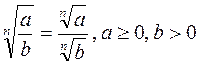
3) ![]()
Уметь доказывать аналитически и проводить графическую иллюстрацию следующего свойства корня n-й степени:
- Значения корня ![]() при
при ![]() возрастают
с возрастанием значений x.
возрастают
с возрастанием значений x.
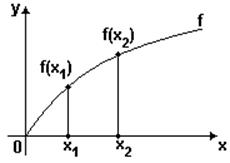 Дано:
Дано: ![]() ,
,![]()
Доказать: ![]()
Доказательство:
1) ![]() - по
определению арифметического корня.
- по
определению арифметического корня.
2) ![]() , так как из
, так как из ![]()
Итак: ![]() .
.
Надо подчеркнуть, что доказательство
данного свойства корня n-й
степени есть суть доказательства монотонности функции, заданной формулой ![]() при
при ![]() .
.
Теперь прежде чем перейти к определению степени с рациональным показателем, следует ввести понятие показательной функции с областью определения Z.
Учащимся необходимо предложить
построить графики нескольких функций, заданных формулой вида: ![]() , где x и y – переменные и
, где x и y – переменные и ![]() , при различных значениях
, при различных значениях ![]() , кроме
, кроме ![]() =0. Надо также рассмотреть случаи: а<0, 0<a<1, a=1, a>1. В начале нужно составить таблицы
значений переменных x и y, вычисленных по формуле
=0. Надо также рассмотреть случаи: а<0, 0<a<1, a=1, a>1. В начале нужно составить таблицы
значений переменных x и y, вычисленных по формуле ![]() (листки
с таблицей можно составить заранее):
(листки
с таблицей можно составить заранее):
|
|
|
|
|
||||
|
x |
y |
x |
y |
x |
y |
x |
y |
|
-3 |
-0,125 |
-3 |
8 |
-3 |
1 |
-3 |
0,125 |
|
-2 |
0,25 |
-2 |
4 |
-2 |
1 |
-2 |
0,25 |
|
-1 |
-0,5 |
-1 |
2 |
-1 |
1 |
-1 |
0,5 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
-2 |
1 |
0,5 |
1 |
1 |
1 |
2 |
|
2 |
4 |
2 |
0,25 |
2 |
1 |
2 |
4 |
|
3 |
-8 |
3 |
0,125 |
3 |
1 |
3 |
8 |
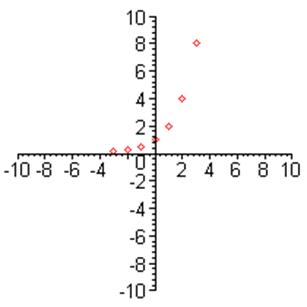
1. График функции ![]() : 2. График
функции
: 2. График
функции 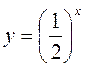 :
:
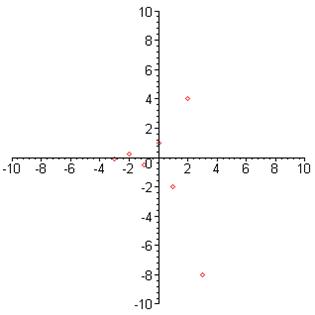
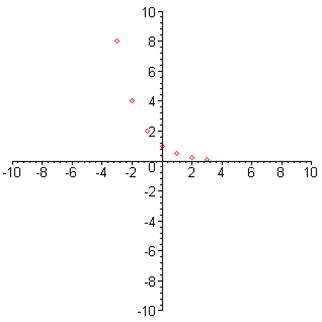
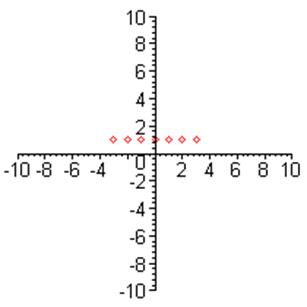
3. График функции ![]() : 4. График
функции
: 4. График
функции ![]() :
:
На основе анализа соответствующих таблиц и графиков учащихся нужно подвести к предположению, что справедливы следующие свойства функций:
1) При a>0 функция, заданная формулой ![]() , где
, где ![]() ,
принимает положительные значения.
,
принимает положительные значения.
2) При a>1 функция, заданная формулой ![]() , где
, где ![]() ,
возрастает; при 0<a<1 –
убывает.
,
возрастает; при 0<a<1 –
убывает.
Затем провести доказательство этих свойств, опираясь на свойства степени с целым показателем. При ведении записи доказательства учащиеся должны приводить использованное свойство степени с целым показателем или его существенные признаки, а не указывать только его порядковый номер. Например, запись доказательства второго свойства при a>1 можно сформировать так:
Дано: ![]()
Доказать: f – возрастающая.
Доказательство:
1.
![]() и
и ![]() .
.
2.
f – возрастающая, если для любых
значений аргумента из ![]() , то есть из
, то есть из ![]() .
.
3.
![]() , так как
, так как ![]() при
при ![]() и
и ![]() .
.![]()
4.
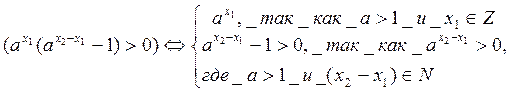
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.