





Лекция 3
Тема: Математические понятия и способы их определения.
План
1. Сущность понятия. Содержание понятия и его объем.
2. Определение понятий.
3. Ошибки в определениях.
4. Методика изложения определений.
1. Сущность понятия. Его содержание и объем.
Познание реальной действительности осуществляется в диалектическом единстве чувственной и рациональной форм мышления. К чувственной форме деятельности относятся ощущения, восприятия, представления.
Восприятием называется непосредственное чувственное отражение
действительности в сознании человека.
Представлением называется запечатленный в нашем сознании образ предмета или явления, в данный момент нами не воспринимаемого.
К рациональной форме мышления, в которой относятся понятия, суждения, умозаключения.
Понятие – форма мышления, в которой отражаются существенные признаки объектов реального мира.
Термин "понятие" используется для обозначения мысленного образа некоторого класса вещей, процессов, отношений объективной реальности или нашего сознания.
Можно сказать, что понятие есть результат обобщения восприятий и представлений очень большого количества однородных явлений и предметов.
Математические понятия отличаются высокой степенью абстрактности. Это обстоятельство послужило поводом для ошибочных представлений о математике, как о науке, в которой человек имеет дело с продуктами свободного творчества разума.
Понятие всегда включает в себя существенные признаки данного множества объектов.
Существенными признаками понятия называются такие признаки, каждый из которых необходим, а все вместе достаточны, чтобы отличить объекты данного рода от других объектов.
Пусть Р1, Р2, ……….Рn есть существенные признаки понятия Р. Это означает следующее:
1. если какой-нибудь отдельный объект не обладает хоть одним из этих признаков, то он не входит в понятие Р.
2. если какой-нибудь отдельный объект обладает всеми этими признаками, то он входит в понятие Р.
Существенные признаки параллелограмма:
1. Четырехугольник;
2. противоположные стороны параллельны;
3. противоположные стороны равны;
4. диагонали в точке пересечения делятся пополам;
5. противоположные углы равны и т.д.
При определении понятия параллелограмм указываются не все существенные признаки, а можно ограничиться признаками 1-2 (либо 1 и 3) (либо 1 и 4).
Признаки входящие в определение понятия должны быть независимыми.
В каждом понятии различают его содержание и его объем.
Содержанием понятия называется совокупность существенных признаков, объектов, охватываемых понятием.
Объемом понятия называется совокупность объектов, на которые распространяется данное понятие.
Понятие "человек".
Содержание понятия: живое существо, создает орудия производства, обладает способностью абстрактного мышления.
Объем: все люди земного шара.
Понятие "тетраэдр".
Содержание: многогранник, ограничен четырьмя гранями, имеющими форму треугольников.
Объем: множество всех тетраэдров.
Понятие "параллелограмм" (содержание, объем понятия).
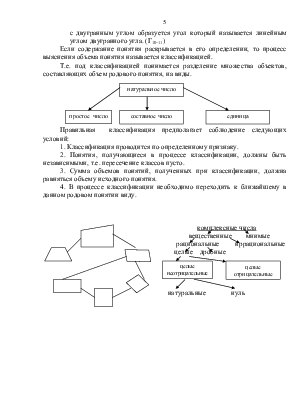
Числовое множество (объем).
Между объемом и содержанием понятия существует такое соотношение: чем больше содержание, тем меньше его объем.
Понятие "прямоугольник". Объем: все прямоугольники.
Добавим новый признак - равенство прилежащих сторон, тогда объем сократится, в него войдут только квадраты.
Если объем одного понятия входит как часть в объем другого понятия, то первое понятие называется видовым, а второе родовым.
V1 Ì V2
видовое понятие родовое понятие
Понятно, что названия "род" и "вид" имеют относительный характер.
![]() V "прям.призмы" Ì V "призмы"
Ì "многогранники"
V "прям.призмы" Ì V "призмы"
Ì "многогранники"
родовое понятие видовое понятие
Отношение между родовым и видовым понятием можно выразить следующим образом.



 род призма вид прямая призма
род призма вид прямая призма
В процессе конструирования определений приходится совершать переходы как от вида к роду (обобщение понятия), так и от рода к виду
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.