Методика изучения действительных чисел. О необходимости изучения действительных чисел в школьном курсе

Методика изучения действительных чисел.

План:

1.  О необходимости изучения действительных чисел в школьном курсе.

2.  Введение иррационального числа в восьмилетней школе.

3.  Изучение действительных чисел в 10 классе.

1.  О необходимости изучения действительных чисел в школьном курсе.

Нет другого раздела школьного курса математики, который усваивался бы с таким трудом, как раздел, посвященный переходу от множества рациональных чисел к множеству действительных, осуществляемых в 8 классе через введение иррациональных чисел.

На вопрос о том, что же такое иррациональное число, часто выпускники школ отвечают, что это корень. Считают, что если  и  сложить можно, то сумму чисел  и  определить нельзя. Если при решении квадратного уравнения абитуриент получает в ответе числа , то считают, что уравнение составлено неверно.

Обойтись без иррационального числа в курсе элементарной математики нельзя, но ни одна из существующих теорий действительных чисел по своей сложности неприемлема в школе. Поэтому учащиеся знакомятся с действительными числами в ознакомительном порядке.

Действительные числа в школьном курсе изучаются дважды: при введении иррационального числа в курсе А-8 и в 10 классе этой теме посвящен параграф 1 (2 пункта). Необходимость изучения множества действительных чисел в школьном курсе диктуется, прежде  всего, потребностями самого курса математики.

Изучением множества R завершается рассмотрение числовых множеств в школьном курсе. Понятие действительного числа лежит в основе метрической геометрии и измерения геометрических величин. Без понятия действительного числа нельзя четко определить понятия предела числовой последовательности и функции, иными словами – нельзя ввести начала анализа, предусмотренные программой.

2.  Введение иррационального числа в восьмилетней школе.

Первое знакомство учащихся с иррациональными числами происходит в курсе алгебры 8 класса в теме «Квадратные корни».

Параграф 20 «Арифметический квадратный корень». Основная цель: ввести определение квадратного корня, арифметического квадратного корня, показать алгоритм доказательства того, что число является арифметическим квадратным корнем.

Понятие квадратного корня и арифметического квадратного корня появляются в ходе решения задачи на нахождения стороны квадрата по известной его площади. Важно, чтобы учащиеся хорошо усвоили, что символ  вводится только для арифметического квадратного корня, обозначающего неотрицательный корень уравнения . Число, противоположное арифметическому корню, обозначается .    и только, но .

Учащиеся должны уяснить, что  есть число неотрицательное. После того, как сформулировано первоначальное представление об арифметическом квадратном корне из числа  и введен символ , можно поставить вопрос о том, при каких значениях переменной  выражение  имеет смысл. При  - смысла нет (из определения ). Квадратный корень из ,  это такое неотрицательное число, квадрат которого равен .

Но при любом ли  определено выражение ?

В связи с постановкой этого вопроса естественным образом вводятся в рассмотрение такие выражения, как  и т.д.

Алгоритм проверки факта, что данное число  состоит из 2 шагов: 1). ; 2).. Для отработки этого алгоритма – упражнение №241.

Упражнение №239. Какое из указанных равенств является верным?

Упражнение №252. При каком значении  верно равенство: .

Упражнение №313. При каком значении  имеет смысл выражение .

Параграф 21 посвящен понятию действительного иррационального числа и приближенному вычислению квадратных корней.

Натуральные числа

Целые числа

Рациональные числа

Положительные рациональные числа

Иррациональные числа

Иррациональные числа

Натуральные Целые Рациональные

Цель: познакомить учащихся с понятием иррационального числа, с множеством действительных чисел и обобщить имеющиеся у учащихся представления о числовых множествах.

 

Таблица 1                                                                                                                                   Таблица 2.

Запись рациональных и иррациональных чисел в виде бесконечной десятичной дроби. Рациональное число – бесконечная периодическая  и конечная дробь. Иррациональное число – бесконечная непериодическая дробь. Пример: 0,1010010001. Бесконечные десятичные непериодические дроби называют иррациональными числами.

           - примеры иррациональных чисел, одна из форм их записи. Нельзя сказать: корни квадратные называются иррациональными числами. Требовать доказательства того факта, что  есть иррациональное число, не следует. Учащиеся знакомятся с одним приближенным методом извлечения  (так называемый метод проб).

            разделим на 10 равных частей

      2,0        2,1       2,2       2,3

 

      4,0     4,41      4,84     5,29    2,2<<2,3

 разделим на 10 равных частей

         2,20        2,21         2,22       2,23      2,24

 

      4,8400     4,8841    4,9284  4,9729  5,0176

2,23 <<2.24          

Изучая тождество , свойства корней, следует обращать внимание учащихся на запись точного и приближенного результата. Учащиеся должны четко представлять, что  есть число, записанное в виде суммы двух иррациональных чисел, можно найти его приближенное значение.

3.  Изучение действительных чисел в 10 классе.

Тема «Действительные числа» изучается в курсе алгебры и начала анализа 10 класса, является вспомогательной для изучения элементов математического анализа. В 10 классе расширяются возможности приведения различных форм записи иррациональных чисел.

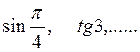. При изучении логарифмической функции появляется еще одна форма записи иррациональных чисел

Учащиеся должны знать, что любое рациональное число может быть представлена в виде бесконечной периодической дроби, быть представлено в виде бесконечной непериодической дроби.

В учебнике предлагается учащимся одна довольно оригинальная форма обращения периодической десятичной дроби в обыкновенную.

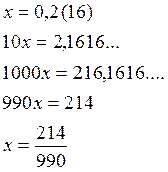
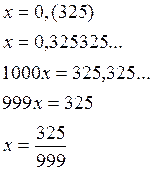
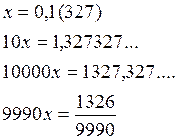
Столько цифр «9» в знаменателе, сколько цифр в периоде. Сколько нулей в знаменателе, сколько цифр до периода. Действия над действительными числами. Изображение действительных чисел на числовой оси.