15. Системы линейн. ур-ий
Пусть имеем линейн. с-му ур-ий вида
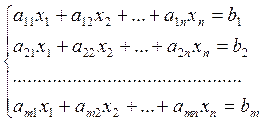
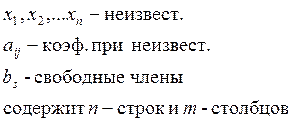
Таблица, составленная из коэффициентов при неизвестных называется матрицей с-мы.
Матрица одностолбцовая состоит только из свободных членов, расширенная состоит из коэффициентов при неизвестных и свободных членов.
О: Если в системе все свободные члены
равны 0, то система однородная. Если хотя бы один из коэффициентов не
равен 0, то — неоднородная. Решение системы- набор из п
чисел ![]() таких, что если
таких, что если ![]() заменить
на
заменить
на ![]() с тем же набором в системе то получим
верное рав-во. (
с тем же набором в системе то получим
верное рав-во. (![]()
![]() )
)
Если с-ма имеет решение то она назыв. совместной(1 единатвен. решение (определённый); бесконечно много(неопределённое), не имеет- несовмест.
О:2 с-мы равносильны тогда и только тогда, когда они имеют одинаковое мн-во решений.
Элементарные преобразования с-м ур-й, теорема о равносильности:
1. поменять местами ур-ие си-мы
2. умножить любое ур-ие на число отличное то 0
3. умножить любое ур-ие на любое число и «+» к любому другому ур-ию
Т: Любое из элементарн. преобразований с-мыпреобразует с-му в равносильную ей с-му.
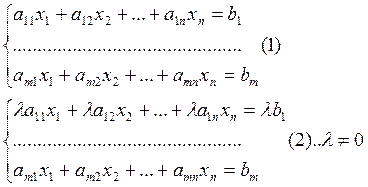
М- мн-во реш-й с-мы (1)
К*- мн-во реш-й с-мы (2)
Т.д. М=К*
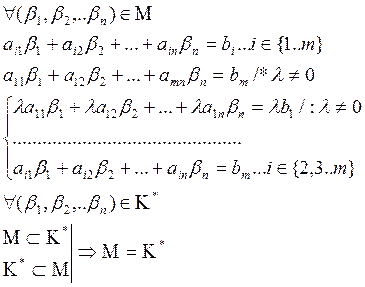
Проведём
рассуждение в обратном порядке, имеем си-му (1) вторе ур-ие «*» на ![]() и прибавим к первому
и прибавим к первому
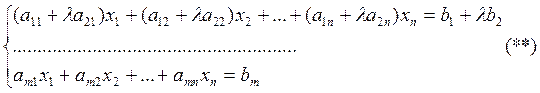
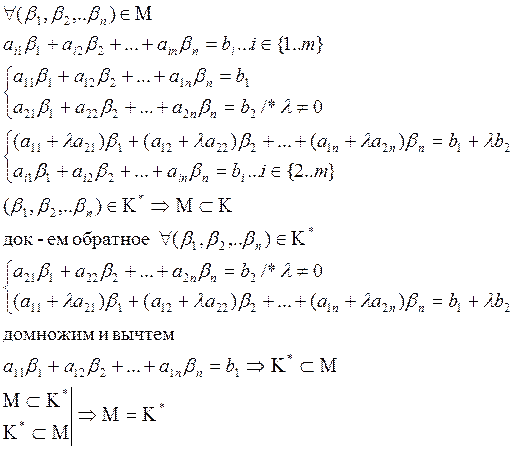
Т: Если к с-ме (1) применить конечное число элементарн. преобразований 1-3 то получ. с-ма равносильная исходной.
Док-во: методом мат. индукции.
Б.И. к=1 теорема верна
Ш.И.
при каком то натуральном к теорема
верна, док-ем что теорема верна если применить (к+1) преобразование ![]()
МЕТОД ГАУСА
Пусть имеем с-му (1), среди эл-ов первого столбца есть хоть один отличный от 0
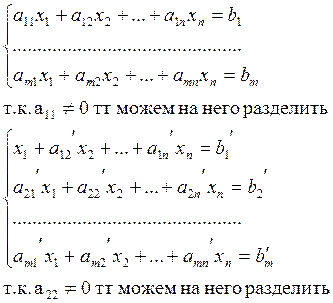
В ходе преобразований получим
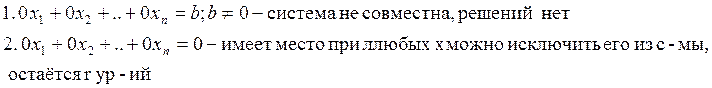
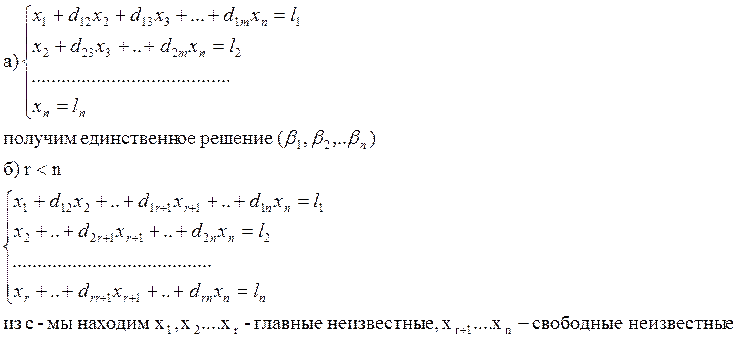
Частным решением назыв. решение кот. получена из общего решения при произвольном наборе свободных эл-ов.
ПРАВИЛО КРАММЕРА
Применяется : когда число ур-ий равно числу неизвестных, rand основной матрицы равен п
Имеем с-му
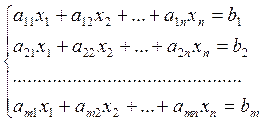
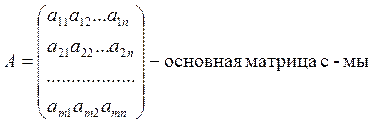
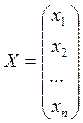
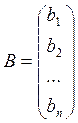
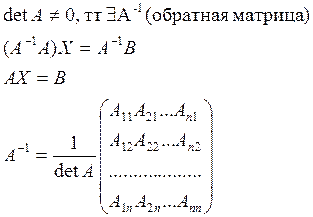
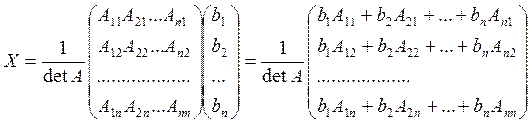
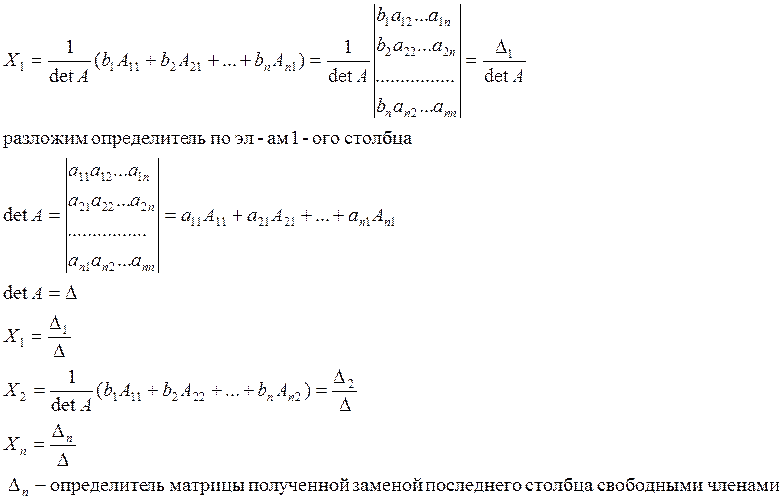 Применимость
Применимость
1.
![]()
2. с-ма имеет единственное решение
Критерий совместности с-м ур-й (теорема Кронекера-Капелли)
С-ма линейн. ур-ий совместна тогда и только тогда, когда rang основной матрицы равен rang расширенной матрицы этой с-мы.
Реал-я осн-х принципов дид-ки при из-и систем уравнений.
Сис-мы двух ур-й из-ся в 7кл. 8 кл. с 2-я неизвестными Ввод-ся пон-е решения систем ур-й. Рассм-ся способы решения: способ подстановки, способ сложения, граф-й способ решения систем ур-й. Решение задач с пом. систем ур-й.
Система ур-ий может состоять из нескольких уравнений с несколькими перемен-
ными. В школе изучаются системы уравнений с двумя переменными. Решить с-му с двумя переменными — это значит найти все пары (х,у), которые
удовлетворяют каждому из
заданных уравнений. Система
называется определенной,
если она имеет конечное число решений, и неопределенной, если она имеет бесконечное множество решений. При решении
системы уравнений можно
от данной системы переходить
к равносильной системе и так далее, пока решение системы не будет получено или будет очевидно, что данная система
не имеет решений. Две
системы называются равносильными,
если они имеют одно и то же множество решений. Систему уравнений можно решать графически. Прежде чем решать с-му линейн.
ур-ий, можно определить число её решений 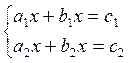 .
.
Если коэф. при х и у не
пропорциональны, то с-ма имеет единствен. решение 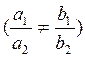 если
решать графически, то гр. ф-ий пересекутся в одной точке. Коэф. при х и у
пропорциональны, а свободные члены не пропорцион. то с-ма не имеет решение
если
решать графически, то гр. ф-ий пересекутся в одной точке. Коэф. при х и у
пропорциональны, а свободные члены не пропорцион. то с-ма не имеет решение 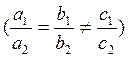 гр. параллельные прямые. Коэф. при х
и у и свободные члены пропорциональны, то с-ма имеет бесконечное
мн-во решение
гр. параллельные прямые. Коэф. при х
и у и свободные члены пропорциональны, то с-ма имеет бесконечное
мн-во решение 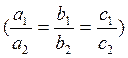 .
.
Способы решений ур-ий
1. подстановки (в одном из уравнений выражают одну переменную через другую. Полученное выражение подставляют в другое уравнение, которое после этого обращается в уравнение с одной переменной, а затем решают его. Получившиеся значения этой переменной подставляют в любое уравнение исходной системы и находят вторую переменную.)
2. сложения (если данная система состоит из уравнений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.