Первичное исследование временных рядов с помощью показателя Херста, фрактальной размерности и старшего показателя Ляпунова

ПЕРВИЧНОЕ ИССЛЕДОВАНИЕ ВРЕМЕННЫХ РЯДОВ С ПОМОЩЬЮ ПОКАЗАТЕЛЯ ХЕРСТА, ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ И СТАРШЕГО ПОКАЗАТЕЛЯ ЛЯПУНОВА

г. Комсомольск-на-Амуре,

ФГОУ ВПО «АмГПГУ»

Введение

Прежде чем заниматься задачей прогнозирования временного ряда (ВР - это упорядоченная во времени последовательность данных), нужно подобрать оптимальные методы. А для этого нужно знать какую природу имеет исследуемый ряд (персистентный, антиперсистентный или  броуновский процесс).  Если процесс относиться к хаотическому (антиперсистентному), то важно знать его горизонт предсказуемости.

Для первоначального исследования используются различные показатели, например показатель Херста, фрактальная размерность [1],  показатель Ляпунова [2,3]. Данные показатели позволяют определить к какому из трёх типов относиться временной ряд.

Фрактальная размерность (ФР)

Особенности временных рядов и их изменения могут быть определены с помощью теории фракталов.  Размерность Хаусдорфа-Безиковича или ФР позволяет упорядочивать исследуемые процессы по свойствам хаотичности или сложности.

Размерность Хаусдорфа-Безиковича для компактного множества в произвольном метрическом пространстве вычисляется по формуле: 

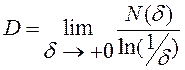
где -  минимальное количество шаров радиуса  , покрывающих это множество.

Для большинства ВР естественных процессов возможно нахождение только численного значения ФР, через величины, связанные с ней простым соотношением, например, через показатель Херста.

Показатель Херста (H)

Показатель Херста, для гауссовых процессов связан с ФР соотношением .

Выделяют три различных типа значений показателя Херста:[1]

1.   Персистентное (поддерживающееся) поведение ВР.

Персистентные стохастические процессы имеют четко выраженные тенденции изменения. Это значит, что если значения ВР увеличивались в течение времени t, то можно ожидать их увеличения в течение последующего периода примерно такой же длительности. И наоборот, если значения ВР уменьшаются в течение времени t, то следует ожидать их дальнейшего уменьшения в течение последующего такого же интервала времени.

2.  Антиперсистентное поведение ВР.  

При таком значении H , после возрастания ВР обычно происходит его уменьшение, а после уменьшения-возрастание. Такое поведение характерно для фрактальных броуновских процессов.

3. 

Такое значение указывает на то, что ряд является случайным. Примером такого ВР является броуновское движение. Такие ВР плохо поддаются прогнозированию.

Вычисление показателя Херста:

1. Сначала вычисляются отклонения от среднего значения:

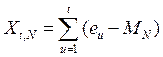
где  – длина периода, меняющаяся от 2 до <длины временного ряда>; – переменная, меняющая своё значение от 1 до ;  – среднее  элементов; – конкретный элемент временного ряда.

2. На каждой итерации мы получаем  значений , которые мы используем в следующей формуле:

где  – размах отклонения .

3. Далее мы нормируем размах делением на стандартное отклонение , которое вычисляется по значениям.

4. Логарифмируем  и  и строим на основании полученных данных график.

5. По графику функции от находим наклон путём линейной аппроксимации.

Тангенс угла этого наклона и является показателем Хёрста.

Показатель Ляпунова

Если старший показатель Ляпунова (СПЛ) больше нуля, это говорит о хаотической динамике временного ряда [4] и отражает чувствительную зависимость динамической системы от начальных данных. Нулевое значение  СПЛ говорит о том, что динамику хаоса можно описать системой нелинейных дифференциальных уравнений. А отрицательное значение СПЛ, отмечает снижение нестационарности [2]. Значение показателя Ляпунова обратно пропорционально времени, на которое можно предсказать состояние системы с  динамическим хаосом.

Рассмотрим отображение .  [3] Под его действием точки могут разбегаться, что ведёт к хаотическому движению. Согласно, рисунку 1 имеем: 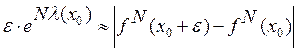 , где  - показатель Ляпунова.

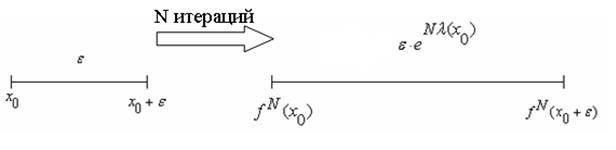
Рис.1. Определение показателя Ляпунова.

Тогда показатель Ляпунова определяется выражением:

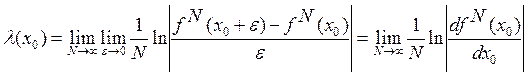
Заключение

В работе рассмотрены показатели (H,D) позволяющие отнести исследуемый ряд к одному из трёх процессов (персистентный, антиперсистентный или  броуновский).  Также рассмотрен показатель Ляпунова, который позволяет определить наличие хаотической динамики.  С показателем Ляпунова связан горизонт предсказуемости хаотической системы: за время обратно пропорциональное показателю Ляпунова система полностью теряет   информацию о своем начальном состоянии. Таким образом, прогноз динамики хаотической системы на временах больших горизонта предсказуемости в принципе невозможен.

Библиографический список:

1.  Федер Е. Фракталы: Пер. с англ.-М.: Мир, 1991.-254 с.

2.  Хайкин С.  Нейронные сети: полный курс, 2-e издание. : Пер. с англ. М. Издательский дом "Вильямс", 2006. 1104 с.

3.  Шустер Г. Детерминированный Хаос. – М.:Мир, 1988. – 240 с.

4.  Кузнецов С.П. Динамический хаос . (курс лекций): Учебное пособие для вузов. 2-е изд. перераб. и доп. – М.: издательство Физико-математической литературы, 2006.- 356 с.